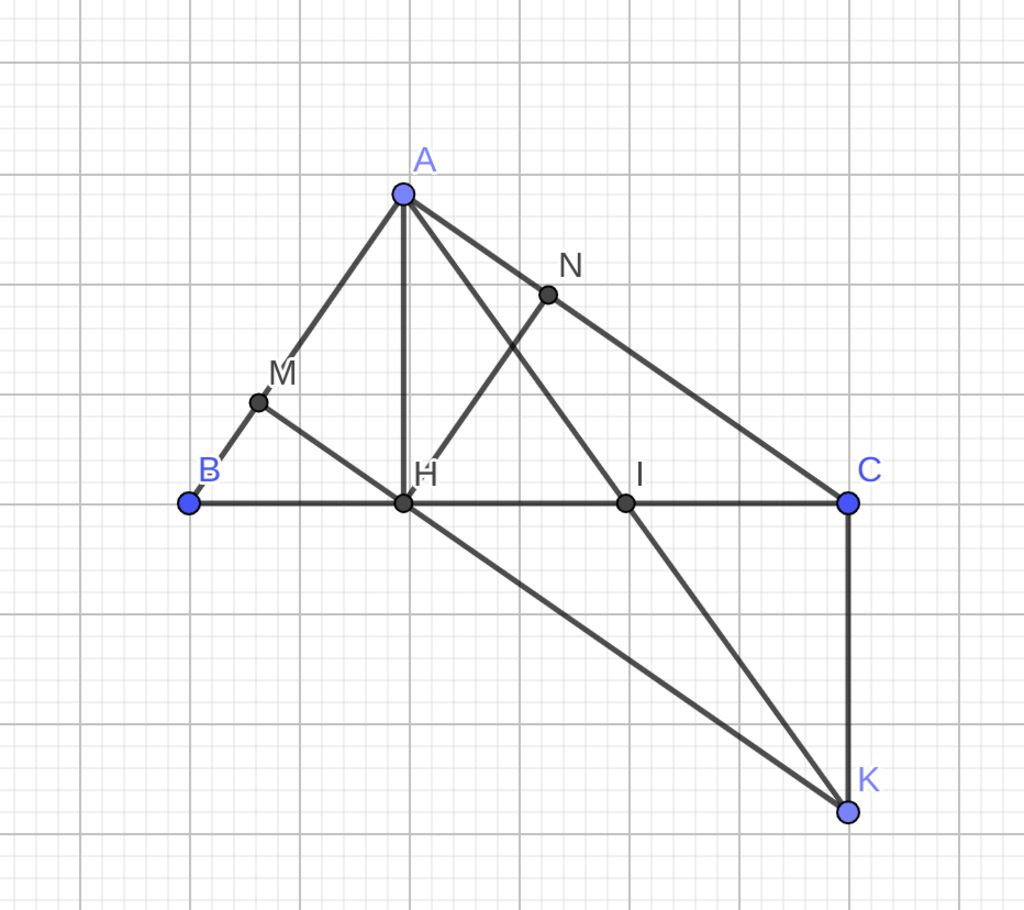
Để giải bài toán này, chúng ta sẽ xem xét tứ giác \( AMHN \) và chứng minh các yêu cầu.

### a) Tứ giác \( AMHN \) là hình gì? Vì sao?

Tứ giác \( AMHN \) là một hình chữ nhật.

**Giải thích:**
- Vì \( H \) là chân đường cao từ \( A \) xuống cạnh \( BC \) của tam giác vuông \( ABC \), do đó \( AH \) vuông góc với \( BC \).
- \( HM \) vuông góc với \( AB \) và \( HN \) vuông góc với \( AC \).
- Do đó, cả hai cặp cạnh \( AM \) và \( AH \), \( AN \) và \( AH \) đều vuông góc với nhau.
- Hơn nữa, trong một tam giác vuông, đường cao chia tam giác thành hai tam giác nhỏ cũng vuông, vì vậy \( \angle AMH = 90^\circ \) và \( \angle ANH = 90^\circ \).

Vì vậy, tứ giác \( AMHN \) có hai cặp cạnh vuông góc, từ đó suy ra \( AMHN \) là hình chữ nhật.

### b) Chứng minh \( MN = AH \)

Để chứng minh \( MN = AH \), chúng ta có thể sử dụng các tính chất của tam giác vuông và định lý đường cao.

1. **Xem xét tam giác \( AMH \):**
- Trong tam giác vuông \( AHB \), \( AH \) là đường cao.
- Theo định lý đường cao, ta có:
\[
AH^2 = AM \cdot AN
\]

2. **Xem xét tam giác \( HMN \):**
- \( HM \) vuông góc với \( AB \) và \( HN \) vuông góc với \( AC \), do đó tam giác \( HMN \) cũng vuông tại \( H \).
- Sử dụng định lý Pythagore cho tam giác vuông \( HMN \):
\[
MN^2 = HM^2 + HN^2
\]

3. **So sánh các đoạn:**
- \( AM \) và \( AN \) là các cạnh trong tam giác vuông \( AHB \), vì vậy khi sử dụng các tính chất của tam giác vuông và đường cao, ta có thể thấy rằng \( MN \) cũng là chiều cao từ \( H \) xuống cạnh \( AN \) và \( AM \).
- Bằng việc xem xét các tam giác tương ứng và tính chất vuông góc, ta thấy rằng \( MN = AH \).

### Kết luận
Tứ giác \( AMHN \) là hình chữ nhật và \( MN = AH \).