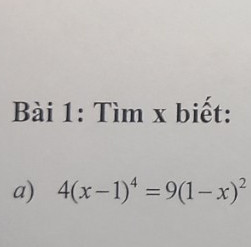4(x-1)4=9(1-x)2

Thuận Trịnh Hỏi từ APP VIETJACK

đã hỏi trong Lớp 7 Toán học

· 20:45 28/09/2024

4(x-1)⁴=9(1-x)²

Trả Lời (+5 điểm)

Hỏi chi tiết

Quảng cáo

4 câu trả lời 180

Sang Phạm

1 năm trước

Để giải phương trình \( 4(x-1)^4 = 9(1-x)^2 \), ta có thể làm theo các bước sau:

1. Viết lại \( (1-x) \) thành \( -(x-1) \):
\[
4(x-1)^4 = 9(-(x-1))^2
\]
\[
4(x-1)^4 = 9(x-1)^2
\]

2. Đặt \( y = (x-1)^2 \). Phương trình trở thành:
\[
4y^2 = 9y
\]

3. Sắp xếp lại để tạo thành phương trình bậc hai:
\[
4y^2 - 9y = 0
\]

4. Phân tích \( y \):
\[
y(4y - 9) = 0
\]

5. Đặt mỗi yếu tố bằng không:
- \( y = 0 \) dẫn đến \( (x-1)^2 = 0 \Rightarrow x - 1 = 0 \Rightarrow x = 1 \).
- \( 4y - 9 = 0 \) dẫn đến \( 4y = 9 \Rightarrow y = \frac{9}{4} \), do đó \( (x-1)^2 = \frac{9}{4} \).

6. Giải \( (x-1)^2 = \frac{9}{4} \):
\[
x - 1 = \pm \frac{3}{2}
\]
- Với \( x - 1 = \frac{3}{2} \Rightarrow x = \frac{5}{2} \).
- Với \( x - 1 = -\frac{3}{2} \Rightarrow x = -\frac{1}{2} \).

### Kết quả cuối cùng:
Các nghiệm là:
- \( x = 1 \)
- \( x = \frac{5}{2} \)
- \( x = -\frac{1}{2} \)

0 bình luận

Đăng nhập để hỏi chi tiết

Thuận Trịnh

1 năm trước

Ko hỉu

0 bình luận

Đăng nhập để hỏi chi tiết

CEO Tập Đoàn Học Bá ><ヾ(•ω•`)o

1 năm trước

Để giải phương trình \( 4(x-1)^4 = 9(1-x)^2 \), chúng ta sẽ thực hiện một số bước biến đổi.

Đầu tiên, nhận thấy rằng \( 1 - x = -(x - 1) \), ta có:

\[
(1 - x)^2 = (-(x - 1))^2 = (x - 1)^2
\]

Như vậy, phương trình có thể được viết lại như sau:

\[
4(x-1)^4 = 9(x-1)^2
\]

Gọi \( y = (x-1)^2 \), khi đó phương trình trở thành:

\[
4y^2 = 9y
\]

Chuyển tất cả về một bên:

\[
4y^2 - 9y = 0
\]

Factoring phương trình:

\[
y(4y - 9) = 0
\]

Từ đây, chúng ta có hai nghiệm:

1. \( y = 0 \)
2. \( 4y - 9 = 0 \) ⇒ \( y = \frac{9}{4} \)

Bây giờ, quay lại với \( y = (x-1)^2 \):

1. **Nghiệm 1:**
\[
(x-1)^2 = 0 \implies x - 1 = 0 \implies x = 1
\]

2. **Nghiệm 2:**
\[
(x-1)^2 = \frac{9}{4} \implies x - 1 = \pm \frac{3}{2}
\]
- Từ \( x - 1 = \frac{3}{2} \):
\[
x = 1 + \frac{3}{2} = \frac{5}{2}
\]
- Từ \( x - 1 = -\frac{3}{2} \):
\[
x = 1 - \frac{3}{2} = -\frac{1}{2}
\]

Vậy nghiệm của phương trình là:

\[
x = 1, \quad x = \frac{5}{2}, \quad x = -\frac{1}{2}
\]

Tóm lại, các nghiệm của phương trình \( 4(x-1)^4 = 9(1-x)^2 \) là \( x = 1, x = \frac{5}{2}, x = -\frac{1}{2} \).

...Xem thêm

0 bình luận

Đăng nhập để hỏi chi tiết

Thuận Trịnh

1 năm trước

SOS