Cho đường tròn (O) và dây AB khác đường kính. Kẻ bán kính OC đi qua trung điểm I của đoạn thẳng AB. Vẽ đường tròn (C; CI). Kẻ tiếp tuyến BD của đường tròn (C) với D là tiếp điểm và D khác I. Chứng minh:
a) Bốn đỉnh của tứ giác BDCI cùng nằm trên một đường tròn;
b) BD là tiếp tuyến của đường tròn (O).
Quảng cáo
1 câu trả lời 181
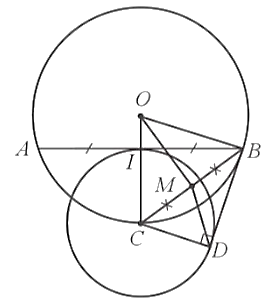
a) Gọi M là trung điểm của đoạn thẳng BC, khi đó
Xét ∆OAB có OA = OB nên ∆OAB cân tại O, suy ra đường trung tuyến OI đồng thời là đường cao của tam giác, hay OC ⊥ AB tại I.
Ta có ∆BIC vuông tại I có IM là đường trung tuyến ứng với canh huyền BC nên
Ta có ∆BDC vuông tại D có DM là đường trung tuyến ứng với canh huyền BC nên
Từ (1), (2) và (3), suy ra
Do đó bốn đỉnh của tứ giác BDCI cùng nằm trên đường tròn đường kính BC.
b) Đường tròn (C) có hai tiếp tuyến BI, BD cắt nhau tại B nên CB là tia phân giác của góc ICD, hay
Mặt khác, ∆OBC cân tại O (do OB = OC) nên hay
Suy ra mà hai góc này ở vị trí so le trong nên OB // CD.
Lại có BD ⊥ CD nên BD ⊥ OB tại B, mà B nằm trên đường tròn (O)
Vậy BD là tiếp tuyến của đường tròn (O).
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
 Đã trả lời bởi chuyên gia
103643
Đã trả lời bởi chuyên gia
103643 -
Hỏi từ APP VIETJACK
 Đã trả lời bởi chuyên gia
68927
Đã trả lời bởi chuyên gia
68927 -
 Đã trả lời bởi chuyên gia
56777
Đã trả lời bởi chuyên gia
56777 -
 Đã trả lời bởi chuyên gia
47628
Đã trả lời bởi chuyên gia
47628 -
 Đã trả lời bởi chuyên gia
44434
Đã trả lời bởi chuyên gia
44434 -
 Đã trả lời bởi chuyên gia
36922
Đã trả lời bởi chuyên gia
36922 -
 Đã trả lời bởi chuyên gia
35490
Đã trả lời bởi chuyên gia
35490


