Question

Đã trả lời bởi chuyên gia

Answer 1

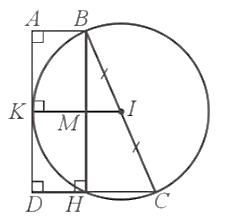
Media VietJack

Kẻ BH vuông góc với CD tại H, gọi I là trung điểm của đoạn thẳng BC, kẻ IK vuông góc với AD tại K, gọi M là giao điểm của IK và BH.

Do IK ⊥ AD nên $\hat{A K I} = \hat{I K D} = 90 ° .$

ABCD là hình thang vuông có $\hat{A} = \hat{D} = 90 °$ nên AB ⊥ AD, CD ⊥ AD.

Mà IK ⊥ AD nên IK // AB // CD.

Lại có BH ⊥ CD nên BH ⊥ IK tại M.

Tứ giác ABHD có $\hat{A} = \hat{D} = \hat{H} = 90 °,$ suy ra ABHD là hình chữ nhật.

Tứ giác ABMK có $\hat{A} = \hat{K} = \hat{M} = 90 °,$ suy ra ABMK là hình chữ nhật.

a) Do tứ giác ABHD là hình chữ nhật nên AD = BH và DH = AB = 4 cm.

Ta có: CH = CD ‒ DH = 9 – 4 = 5 cm.

Xét ∆BCH vuông tại H, theo định lí Pythagore, ta có: BC² = BH² + CH²

Suy ra $B H = \sqrt{B C^{2} - C H^{2}} = \sqrt{13^{2} - 5^{2}} = \sqrt{144} = 12 cm$

Vậy AD = BH = 12 cm.

b) Ta có đường tròn đường kính BC có tâm I và bán kính $R = \frac{B C}{2} = 6, 5 cm.$

Khoảng cách từ tâm I đến AD là d = IK.

Do tứ giác ABMK là hình chữ nhật nên KM = AB = 4 cm.

Xét ∆BCH có I là trung điểm của BC và IM // CH nên IM là đường trung bình của tam giác, do đó $I M = \frac{1}{2} C H = \frac{1}{2} \cdot 5 = 2, 5 cm .$

Ta có: IK = KM + IM = 4 + 2,5 = 6,5 cm.

Do đó d = IM = R = 6,5 cm.

Vậy đường thẳng AD tiếp xúc với đường tròn đường kính BC.

...Xem thêm

Answer 2