Cho đường tròn (O; 3 cm) và (O’; 2 cm) tiếp xúc ngoài với nhau tại A. Một đường thẳng đi qua A cắt (O) và (O’) lần lượt tại B và C (B và C khác A).
a) Chứng minh OB // O’C.
b) Cho AB = 5 cm. Tính độ dài đoạn thẳng AC.
Quảng cáo
2 câu trả lời 204
a) Vì A, B ∈ (O; 3 cm) nên OA = OB = 3 cm.
Do đó ∆OAB cân tại O, suy ra ˆOBA=ˆOABOBA^=OAB^ (1)
Vì A, C ∈ (O’; 2 cm) nên O’A = O’C = 2 cm.
Do đó ∆O’AC cân tại O’, suy ra ˆO′AC=ˆO′CAO'AC^=O'CA^ (2)
Mà (đối đỉnh) ˆO′AC=ˆOABO'AC^=OAB^ (3)
Từ (1), (2), (3) suy ra ˆOBA=ˆO′CAOBA^=O'CA^ hayˆOBC=ˆO′CBOBC^=O'CB^
Mà hai góc này ở vị trí so le trong nên OB // O’C.
b) Vì OB // O’C nên theo định lí Thalès ta có ABAC=OAO′AABAC=OAO'A hay 5AC=32.5AC=32.
Do đóAC=2⋅53=103 cm.
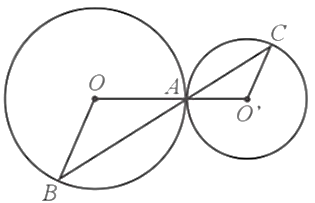
a) Vì A, B ∈ (O; 3 cm) nên OA = OB = 3 cm.
Do đó ∆OAB cân tại O, suy ra (1)
Vì A, C ∈ (O’; 2 cm) nên O’A = O’C = 2 cm.
Do đó ∆O’AC cân tại O’, suy ra (2)
Mà (đối đỉnh) (3)
Từ (1), (2), (3) suy ra hay
Mà hai góc này ở vị trí so le trong nên OB // O’C.
b) Vì OB // O’C nên theo định lí Thalès ta có hay
Do đó
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
 Đã trả lời bởi chuyên gia
103643
Đã trả lời bởi chuyên gia
103643 -
Hỏi từ APP VIETJACK
 Đã trả lời bởi chuyên gia
68927
Đã trả lời bởi chuyên gia
68927 -
 Đã trả lời bởi chuyên gia
56777
Đã trả lời bởi chuyên gia
56777 -
 Đã trả lời bởi chuyên gia
47628
Đã trả lời bởi chuyên gia
47628 -
 Đã trả lời bởi chuyên gia
44434
Đã trả lời bởi chuyên gia
44434 -
 Đã trả lời bởi chuyên gia
36922
Đã trả lời bởi chuyên gia
36922 -
 Đã trả lời bởi chuyên gia
35490
Đã trả lời bởi chuyên gia
35490


