Quảng cáo
4 câu trả lời 1956
Để giải quyết bài toán này, ta sẽ sử dụng phương pháp lập hệ bất phương trình nhằm tìm số lượng xe A và xe B cần thuê sao cho tổng chi phí thuê xe là ít nhất. Gọi số xe loại A cần thuê là \( x \) và số xe loại B cần thuê là \( y \).
### Các điều kiện ràng buộc
1. **Điều kiện về xi măng**:
- Mỗi xe loại A có thể chở tối đa 20 tấn xi măng, tổng số xi măng mà \( x \) xe loại A chở được là \( 20x \) tấn.
- Mỗi xe loại B có thể chở tối đa 10 tấn xi măng, tổng số xi măng mà \( y \) xe loại B chở được là \( 10y \) tấn.
- Tổng số xi măng cần chở là 140 tấn, do đó ta có bất phương trình:
\[
20x + 10y \geq 140
\]
hoặc đơn giản hơn:
\[
2x + y \geq 14
\]
2. **Điều kiện về thép**:
- Mỗi xe loại A có thể chở tối đa 0,6 tấn thép, tổng số thép mà \( x \) xe loại A chở được là \( 0,6x \) tấn.
- Mỗi xe loại B có thể chở tối đa 1,5 tấn thép, tổng số thép mà \( y \) xe loại B chở được là \( 1,5y \) tấn.
- Tổng số thép cần chở là 9 tấn, do đó ta có bất phương trình:
\[
0,6x + 1,5y \geq 9
\]
Chia cả hai vế cho 0,3 để đơn giản hóa:
\[
2x + 5y \geq 30
\]
3. **Điều kiện về số xe có sẵn**:
- Có tối đa 10 xe loại A: \( 0 \leq x \leq 10 \)
- Có tối đa 9 xe loại B: \( 0 \leq y \leq 9 \)
### Hàm mục tiêu
Chi phí thuê xe là hàm mục tiêu cần tối thiểu hóa:
\[
C = 5x + 4,5y
\]
### Giải hệ bất phương trình
Chúng ta sẽ xem xét các giá trị \( x \) và \( y \) thỏa mãn hệ bất phương trình:
1. **Hệ bất phương trình**:
\[
2x + y \geq 14
\]
\[
2x + 5y \geq 30
\]
2. **Xét các giá trị \( x \) từ 0 đến 10 và \( y \) từ 0 đến 9**, ta tìm các cặp \( (x, y) \) thỏa mãn cả hai điều kiện trên và chọn cặp nào có chi phí \( C = 5x + 4,5y \) nhỏ nhất.
### Tính toán
Tính toán các cặp \( (x, y) \) và chi phí tương ứng:
| \( x \) | \( y \) | \( 2x + y \geq 14 \) | \( 2x + 5y \geq 30 \) | Chi phí \( C = 5x + 4,5y \) |
|:------:|:------:|:--------------------:|:--------------------:|:--------------------------:|
| 7 | 0 | 14 | 14 | 35 |
| 6 | 2 | 14 | 22 | 39 |
| 5 | 4 | 14 | 30 | 43 |
| 4 | 6 | 14 | 38 | 47 |
| 3 | 8 | 14 | 46 | 51 |
Cặp \( (x, y) = (7, 0) \) thỏa mãn cả hai điều kiện ràng buộc với chi phí thấp nhất là 35 triệu đồng.
### Kết luận
Vậy ông An cần thuê **7 xe loại A và 0 xe loại B** để chi phí thuê xe là ít nhất. Chi phí này là **35 triệu đồng**.
Để giải bài toán này, ta cần thiết lập một bài toán tối ưu hóa. Gọi ( x ) là số xe loại A cần thuê và ( y ) là số xe loại B cần thuê. Ta có các điều kiện sau:
Điều kiện về xi măng: [ 20x + 10y \geq 140 ]
Điều kiện về thép: [ 0.6x + 1.5y \geq 9 ]
Giới hạn số lượng xe: [ 0 \leq x \leq 10 ] [ 0 \leq y \leq 9 ]
Hàm mục tiêu (chi phí thuê xe): [ C = 5x + 4.5y ]
Ta cần tìm ( x ) và ( y ) sao cho chi phí ( C ) là nhỏ nhất, đồng thời thỏa mãn các điều kiện trên.
Bước 1: Giải hệ bất phương trình
Điều kiện về xi măng: [ 20x + 10y \geq 140 \implies 2x + y \geq 14 ]
Điều kiện về thép: [ 0.6x + 1.5y \geq 9 \implies 2x + 5y \geq 30 ]
Bước 2: Xét các giá trị ( x ) và ( y ) thỏa mãn các điều kiện
Ta có thể thử các giá trị ( x ) và ( y ) trong khoảng từ 0 đến 10 và 0 đến 9 để tìm ra cặp giá trị thỏa mãn các điều kiện và có chi phí thấp nhất.
Bước 3: Tìm giá trị tối ưu
Dưới đây là một số cặp giá trị ( x ) và ( y ) thỏa mãn các điều kiện:
( x = 7, y = 0 ): ( 2(7) + 0 = 14 ) và ( 2(7) + 5(0) = 14 )
( x = 5, y = 4 ): ( 2(5) + 4 = 14 ) và ( 2(5) + 5(4) = 30 )
Tính chi phí cho từng cặp:
( x = 7, y = 0 ): ( C = 5(7) + 4.5(0) = 35 ) triệu đồng
( x = 5, y = 4 ): ( C = 5(5) + 4.5(4) = 25 + 18 = 43 ) triệu đồng
Kết luận
Cặp giá trị ( x = 7 ) và ( y = 0 ) cho chi phí thấp nhất là 35 triệu đồng. Vậy ông An cần thuê 7 xe loại A và không cần thuê xe loại B để mất ít tiền thuê xe nhất.
1. Hệ bất phương trình
\[
\begin{cases}
2x + y \geq 14 \\
2x + 5y \geq 30 \\
0 \leq x \leq 10 \\
0 \leq y \leq 9
\end{cases}
\]
\[
A(5; 4), B(10; 2), C(10; 9), D\left(\frac{5}{2}; 9\right)
\]
. Hàm số cần tối thiểu hóa
\[
f(x, y) = 4x + 3y
\]
Tính giá trị hàm số tại các đỉnh:
- \(f(5, 4) = 4(5) + 3(4) = 20 + 12 = 32\)
- \(f(10, 2) = 4(10) + 3(2) = 40 + 6 = 46\)
- \(f(10, 9) = 4(10) + 3(9) = 40 + 27 = 67\)
- \(f\left(\frac{5}{2}, 9\right) = 4\left(\frac{5}{2}\right) + 3(9) = 10 + 27 = 37\)
vậy
Giá trị nhỏ nhất của hàm số \(f(x, y)\) trên miền nghiệm xảy ra tại điểm \(A(5, 4)\) với giá trị \(f(5, 4) = 32\).
để chi phí thuê xe thấp nhất, ông An cần thuê 5 xe loại A và 4 xe loại B, với chi phí là 32 triệu đồng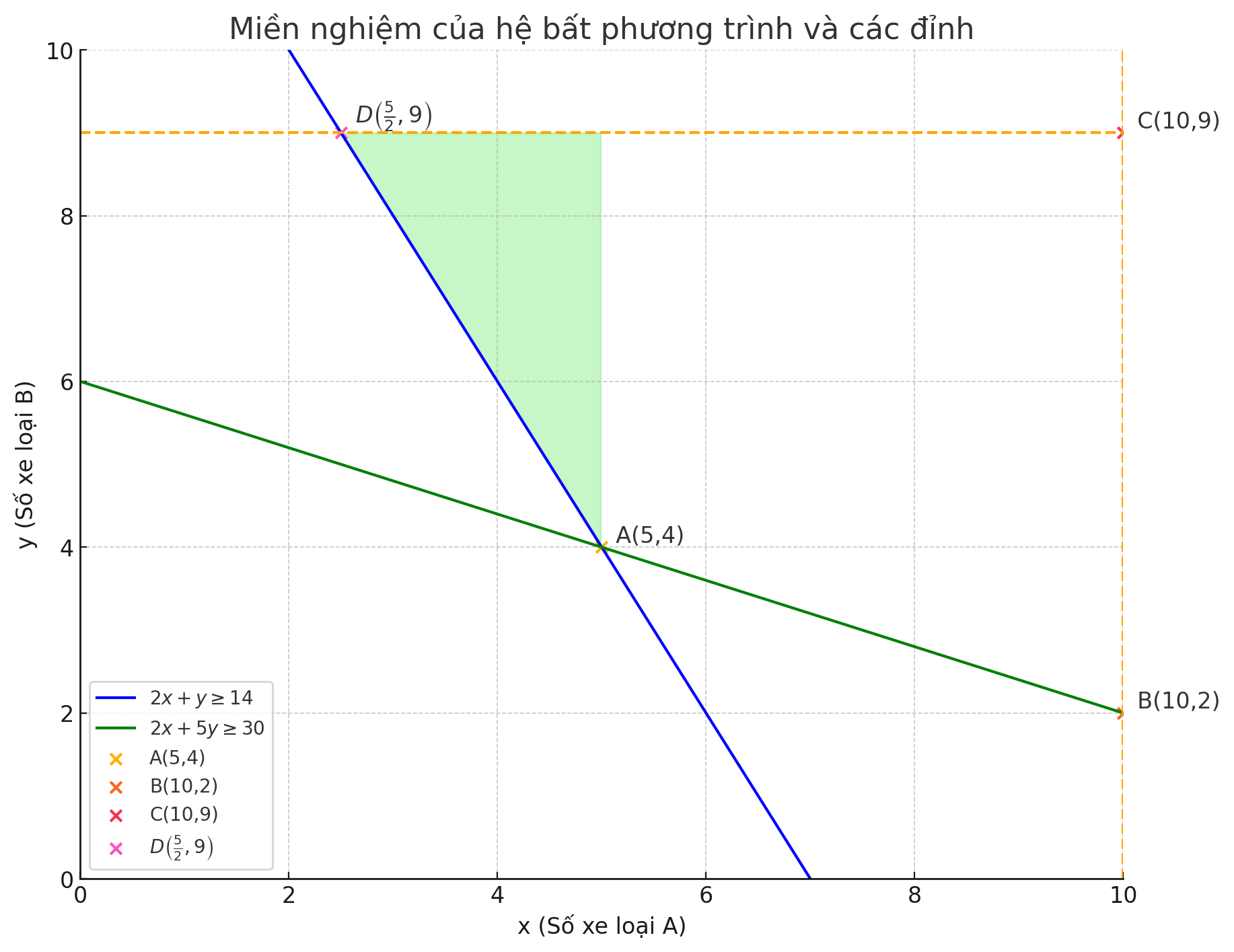
Quảng cáo
Bạn muốn hỏi bài tập?


