Quảng cáo
1 câu trả lời 91
1 năm trước
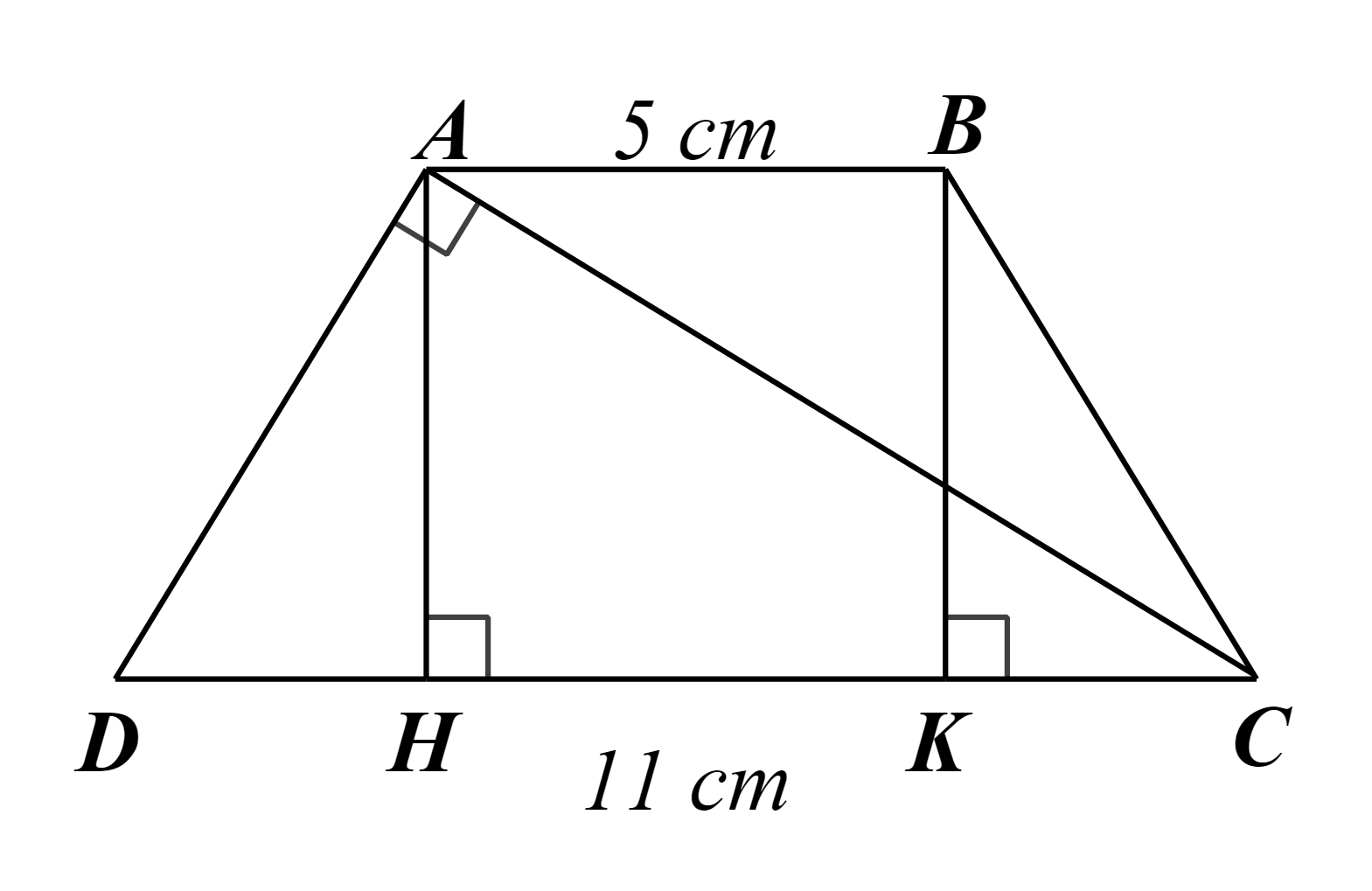
Kẻ AH, BK vuông góc với CD lần lượt tại H, K nên AH ⊥ HK, BK ⊥ HK. Do đó AH // BK.
Do AB // CD, mà H, K ∈ CD nên AB // HK.
Xét tứ giác ABKH có AH // BK và AB // HK nên ABKH là hình bình hành.
Lại có ![]() nên ABKH là hình chữ nhật.
nên ABKH là hình chữ nhật.
Suy ra AH = BK và HK = AB = 5 cm.
Xét ∆ADH (vuông tại H) và ∆BCK (vuông tại K) có:
AD = BC (do ABCD là hình thang cân), AH = BK.
Do đó ∆ADH = ∆BCK (cạnh huyền – cạnh góc vuông).
Suy ra DH = CK (hai cạnh tương ứng).
Mà DH + HK + CK = CD
Nên 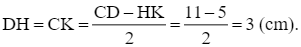
Xét ∆ACD và ∆HAD có:
![]() và
và ![]() là góc chung.
là góc chung.
Do đó ∆ACD ᔕ ∆HAD (g.g)
Suy ra 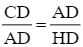 hay AD2 = CD.HD.
hay AD2 = CD.HD.
Vì vậy, ![]()
Quảng cáo
Bạn muốn hỏi bài tập?
Câu hỏi hot cùng chủ đề
-
103437
-
Hỏi từ APP VIETJACK68807
-
56608
-
47524
-
44249
-
36842
-
35274
Gửi báo cáo thành công!


