Cho tam giác ABD (𝐴𝐵𝐷 𝑡ù). Gọi M là trung điểm BD, trên tia đối của tia MA
lấy điểm C sao cho MC = MA.
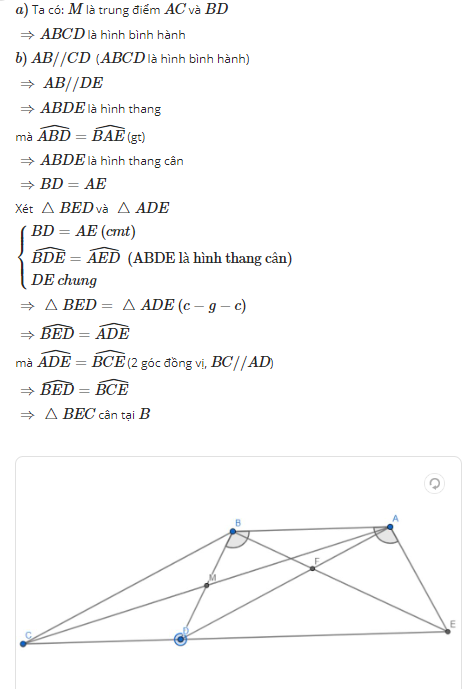
a) Chứng minh tứ giác ABCD là hình bình hành.
b) Trên tia CD lấy E sao cho 𝐴𝐵𝐷= 𝐵𝐴𝐸. Chứng minh: ∆BEC cân tại B.
Quảng cáo
2 câu trả lời 3027
Phần a: Chứng minh tứ giác ABCD là hình bình hành
Giả thiết:
Tam giác ABD có góc ABD là góc tù.
M là trung điểm của BD.
Trên tia đối của tia MA lấy điểm C sao cho MC = MA.
Chứng minh:
Vì M là trung điểm của BD nên ( BM = MD ).
Theo giả thiết, ( MC = MA ).
Xét tam giác ( AMC ) và ( AMD ):( AM ) là cạnh chung.
( MC = MA ) (giả thiết).
( BM = MD ) (M là trung điểm của BD).
Do đó, tam giác ( AMC ) và ( AMD ) bằng nhau theo trường hợp cạnh-cạnh-cạnh (CCC).
Suy ra ( \angle AMC = \angle AMD ).
Vì ( \angle AMC ) và ( \angle AMD ) là hai góc đối đỉnh nên ( \angle AMC = \angle AMD = 180^\circ ).
Do đó, ( AB \parallel CD ) và ( AD \parallel BC ).
Vậy tứ giác ABCD là hình bình hành.
Phần b: Chứng minh tam giác BEC cân tại B
Giả thiết:
Trên tia CD lấy E sao cho ( \angle ABD = \angle BAE ).
Chứng minh:
Xét tam giác ( ABD ) và ( BAE ):( \angle ABD = \angle BAE ) (giả thiết).
( AB ) là cạnh chung.
Do đó, tam giác ( ABD ) và ( BAE ) đồng dạng theo trường hợp góc-cạnh-góc (GCG).
Suy ra ( \angle ABE = \angle ABD ).
Vì ( \angle ABE = \angle ABD ) và ( \angle ABD = \angle BAE ), nên ( \angle ABE = \angle BAE ).
Do đó, tam giác ( BEC ) cân tại B.
Quảng cáo
Bạn muốn hỏi bài tập?