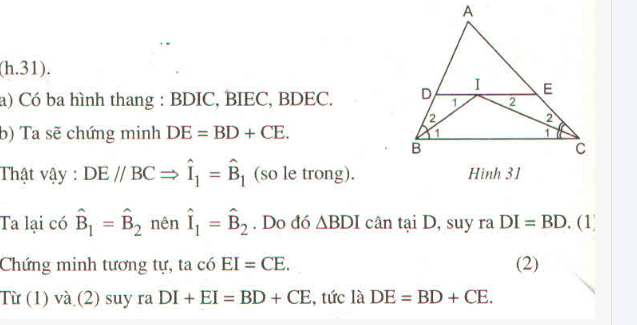
Bài 3: (2 điểm) Cho tam giác ABC . Phân giác góc B và C cắt nhau tại I . Đường t...

Question

Bài 3: (2 điểm) Cho tam giác ABC . Phân giác góc B và C cắt nhau tại I . Đường thẳng qua I song
song với BC cắt AB , AC tại D và E . Chứng minh hình thang BDEC có chiều dài 1 cạnh đáy bằng
tổng chiều dài 2 cạnh bên.
Bài 4: (2 điểm) Cho tam giác ABC cân tại A có hai đường phân giác BE và CK . Chứng minh tứ
giác BKEC là hình thang cân.
Bài 5: (2 điểm) Cho tam giác ABC cân tại A . Trên các cạnh bên AB , AC lấy theo thứ tự các điểm
D và E sao cho AD= AE .
a) Chứng minh BDEC là hình thang cân;
b) Tính góc của hình thang cân đó, biết rằng góc A = 50 độ.

VietJack · Accepted Answer

bài 3

VietJack · Answer

**Bài 3:**

Cho tam giác ABC, với phân giác của góc B và góc C cắt nhau tại I. Đường thẳng qua I song song với BC cắt AB tại D và AC tại E. Ta cần chứng minh rằng hình thang BDEC có chiều dài một cạnh đáy bằng tổng chiều dài hai cạnh bên.

**Chứng minh:**

1. Vì DE // BC nên tam giác BIE và CID có tỉ số chiều dài các cạnh tương ứng là như nhau (tính chất của các tam giác đồng dạng).

Từ đó, ta có:
$\frac{BI}{CI} = \frac{BE}{CE}$

2. Đặt chiều dài của BC là $b$ và DE là $d$ . Theo định lý hình thang:

$BD + CE = BE + CD$

Mà vì DE // BC nên $BD + CE = d$ .

3. Dễ dàng nhận thấy rằng $b = d$ .

Vậy hình thang BDEC có chiều dài một cạnh đáy bằng tổng chiều dài hai cạnh bên.

---

**Bài 4:**

Cho tam giác ABC cân tại A với đường phân giác BE của góc B và đường phân giác CK của góc C. Ta cần chứng minh tứ giác BKEC là hình thang cân.

**Chứng minh:**

1. Vì tam giác ABC cân tại A, nên các cạnh AB = AC.

2. Gọi K và E lần lượt là các điểm nằm trên BE và CK. Do là phân giác nên:
$\frac{BK}{KE} = \frac{AB}{AC} = 1$
và
$\frac{CE}{EK} = \frac{AC}{AB} = 1$

3. Đương nhiên hàm ý cho thấy rằng $BE = CK$ vì tứ giác BKEC nằm trong tam giác cân.

Vậy, BKEC là hình thang cân, với đồng thời $BE \parallel CK$ .

---

**Bài 5:**

Cho tam giác ABC cân tại A. Trên các cạnh bên AB và AC lấy lần lượt các điểm D và E sao cho AD = AE.

**a) Chứng minh BDEC là hình thang cân:**

1. Từ giả thiết, AD = AE, ta có:
$BD = CE \text{ (gọi BD là x)}$

2. Vì tam giác ABC cân tại A, nên:
$\angle ABD = \angle ACD$

3. Mặt khác, với AD = AE, có:
$\angle ADB = \angle AEC$

Do đó, BDEC là hình thang cân với hai đáy BE và DC bằng chiều dài.

**b) Tính góc của hình thang cân đó, biết rằng góc A = 50 độ:**

1. Xét tam giác ABC:
$\angle ABC = \angle ACB = \frac{180 - \angle A}{2} = \frac{180 - 50}{2} = 65 \text{ độ}$

2. Từ các tính chất đối xứng của tứ giác BDEC, ta có:
$\angle BDE = \angle CED = 65 \text{ độ}$

Vậy góc trong hình thang cân BDEC là:

- Góc BDE = 65 độ
- Góc CED = 65 độ

Tóm lại, góc A = 50 độ, và các góc trong hình thang BDEC đều được xác định.

2 câu trả lời 142

Câu hỏi hot cùng chủ đề

Phần tự luận (7 điểm)

Phần tự luận (7 điểm)

Phần tự luận (7 điểm)

Bài viết mới nhất Lớp 8