Quảng cáo
3 câu trả lời 5799
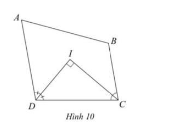
Để tính góc \( D + C \) trong tứ giác \( ABCD \) với các tia phân giác của góc \( D \) và góc \( C \) cắt nhau tại điểm \( I \) tạo thành một góc vuông (180°), ta có thể sử dụng tính chất của tia phân giác.
Theo định lý về tia phân giác trong tứ giác, tổng của các góc ở một tứ giác (khi xét các góc phân giác chúng cắt nhau) được tính như sau:
\[
\angle D + \angle C = 90^\circ + \angle I
\]
Ở đây, vì \( I \) là góc vuông (90°), ta có:
\[
\angle I = 90^\circ
\]
Vậy:
\[
\angle D + \angle C = 90^\circ + 90^\circ = 180^\circ
\]
Do đó, chúng ta có thể kết luận:
\[
\angle D + \angle C = 180^\circ
\]
Tóm lại, tổng của hai góc \( D \) và \( C \) trong tứ giác \( ABCD \) sẽ là \( 180^\circ \).
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
107437
-
Hỏi từ APP VIETJACK
 Đã trả lời bởi chuyên gia
68061
Đã trả lời bởi chuyên gia
68061 -
 Đã trả lời bởi chuyên gia
52846
Đã trả lời bởi chuyên gia
52846 -
 Đã trả lời bởi chuyên gia
47344
Đã trả lời bởi chuyên gia
47344 -
 Đã trả lời bởi chuyên gia
45400
Đã trả lời bởi chuyên gia
45400 -
 Đã trả lời bởi chuyên gia
45045
Đã trả lời bởi chuyên gia
45045 -
Hỏi từ APP VIETJACK
 Đã trả lời bởi chuyên gia
38412
Đã trả lời bởi chuyên gia
38412 -
 Đã trả lời bởi chuyên gia
38191
Đã trả lời bởi chuyên gia
38191