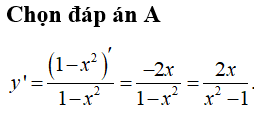Để tìm đạo hàm của hàm số \( y = \ln(1 - x^2) \), ta áp dụng quy tắc chuỗi.

Gọi \( u(x) = 1 - x^2 \), thì hàm số \( y \) có thể viết lại thành:
\[
y = \ln(u(x))
\]

Đạo hàm của hàm số \( y \) theo \( x \) là:
\[
y' = \frac{d}{dx}[\ln(u(x))] = \frac{1}{u(x)} \cdot \frac{du}{dx}
\]

Ta tính \( \frac{du}{dx} \):
\[
\frac{du}{dx} = \frac{d}{dx}[1 - x^2] = -2x
\]

Do đó, đạo hàm của \( y \) là:
\[
y' = \frac{1}{1 - x^2} \cdot (-2x) = \frac{-2x}{1 - x^2}
\]

Vậy, đạo hàm của hàm số \( y = \ln(1 - x^2) \) là:
\[
y' = \frac{-2x}{1 - x^2}
\]

Đạo hàm của hàm số ( y ) phụ thuộc vào dạng cụ thể của hàm số đó. Dưới đây là một số ví dụ về đạo hàm của các hàm số phổ biến:

Hàm số đa thức:

Nếu ( y = x^n ) thì ( y’ = n \cdot x^{n-1} ).
Hàm số mũ:

Nếu ( y = a^x ) thì ( y’ = a^x \cdot \ln(a) ).
Hàm số lượng giác:

Nếu ( y = \sin(x) ) thì ( y’ = \cos(x) ).
Nếu ( y = \cos(x) ) thì ( y’ = -\sin(x) ).
Hàm số phân thức:

Nếu ( y = \frac{ax + b}{cx + d} ) thì ( y’ = \frac{ad - bc}{(cx + d)^2} )