Quảng cáo
2 câu trả lời 281
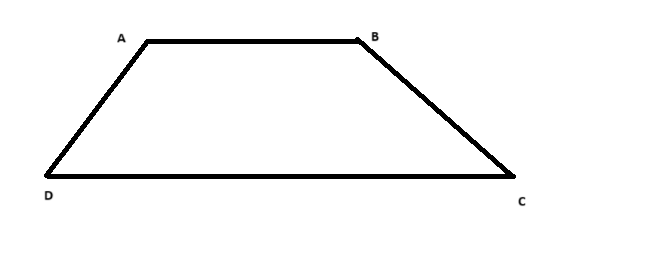
Cho hình thang \(ABCD\) với \(AB \parallel CD\), biết \(\angle D = 60^\circ\) và \(\angle B = 110^\circ\). Ta cần tính các góc \(\angle A\) và \(\angle C\).
**Bước 1: Sử dụng tính chất của hình thang**
Trong hình thang, hai góc kề một cạnh bên sẽ bù nhau, tức là tổng của chúng bằng \(180^\circ\). Cụ thể, ta có:
\[
\angle A + \angle D = 180^\circ
\]
\[
\angle B + \angle C = 180^\circ
\]
**Bước 2: Tính các góc \(A\) và \(C\)**
- Từ \(\angle D = 60^\circ\), ta có:
\[
\angle A = 180^\circ - 60^\circ = 120^\circ
\]
- Từ \(\angle B = 110^\circ\), ta có:
\[
\angle C = 180^\circ - 110^\circ = 70^\circ
\]
**Kết luận:**
Góc \(\angle A = 120^\circ\) và góc \(\angle C = 70^\circ\).
a) Ta có: AB//CD(hai đáy của hình thang ABCD)
nên A^+D^=1800A+D=1800(hai góc trong cùng phía bù nhau)
⇔A^=1800−D^=1800−600⇔A=1800−D=1800−600
hay A^=1200A=1200
Vậy: A^=1200A=1200
b) Ta có: B^D^=45DB=54
⇔B^60=45⇔60B=54
⇔B^=4⋅605=2405=480⇔B=54⋅60=5240=480
Ta có: AB//CD(hai đáy trong hình thang ABCD)
nên B^+C^=1800B+C=1800(hai góc trong cùng phía bù nhau)
⇔C^=1800−B^=1800−480⇔C=1800−B=1800−480
hay C^=1320C=1320
Vậy: B^=480B=480; C^=1320C=1320
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
107593
-
Hỏi từ APP VIETJACK
 Đã trả lời bởi chuyên gia
68300
Đã trả lời bởi chuyên gia
68300 -
 Đã trả lời bởi chuyên gia
52884
Đã trả lời bởi chuyên gia
52884 -
 Đã trả lời bởi chuyên gia
47390
Đã trả lời bởi chuyên gia
47390 -
 Đã trả lời bởi chuyên gia
45461
Đã trả lời bởi chuyên gia
45461 -
 Đã trả lời bởi chuyên gia
45109
Đã trả lời bởi chuyên gia
45109 -
Hỏi từ APP VIETJACK
 Đã trả lời bởi chuyên gia
38488
Đã trả lời bởi chuyên gia
38488 -
 Đã trả lời bởi chuyên gia
38230
Đã trả lời bởi chuyên gia
38230


