Cho hình thoi ABCD có ![]() Gọi M, N, P, Q lần lượt là trung điểm của AB, BC, CD, DA. Chứng minh rằng MBNPDQ là lục giác đều.
Gọi M, N, P, Q lần lượt là trung điểm của AB, BC, CD, DA. Chứng minh rằng MBNPDQ là lục giác đều.
Quảng cáo
1 câu trả lời 161
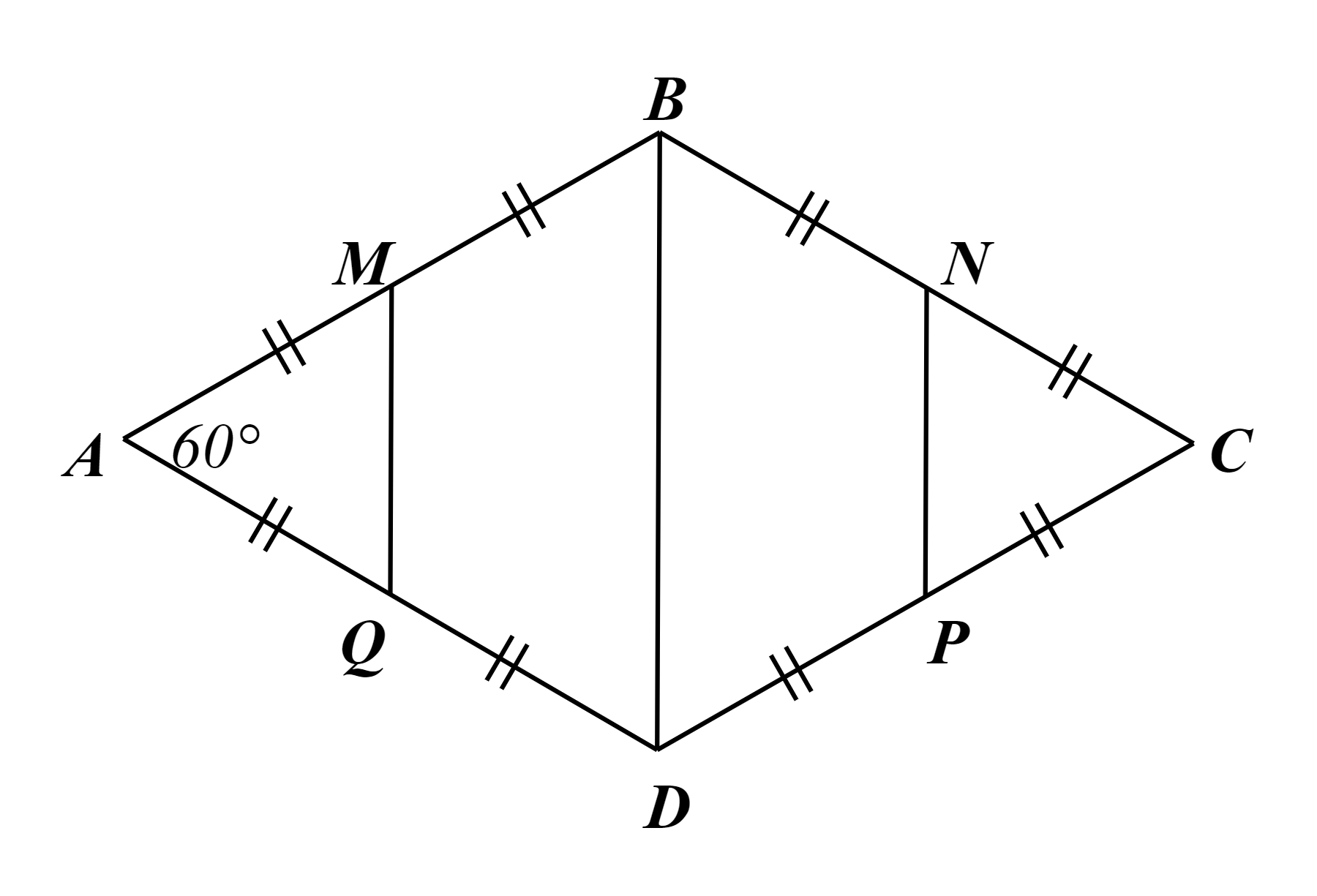
⦁ Vì ABCD là hình thoi nên AB = BC = CD = DA.
Vì M, N, P, Q lần lượt là trung điểm của AB, BC, CD, DA nên ![]()
![]()
![]()
![]()
Do đó ![]()
Xét ∆ABD có AB = AD nên ∆ABD cân tại A, lại có ![]() nên ∆ABD là tam giác đều. Do đó AB = BD (2) và
nên ∆ABD là tam giác đều. Do đó AB = BD (2) và ![]()
Lại có M, Q là lần lượt là trung điểm của AB, AD nên MQ là đường trung bình của tam giác. Do đó MQ // BD và ![]()
Chứng minh tương tự, ta cũng có ![]()
Từ (1), (2), (3) và (4) suy ra MB = BN = NP = PD = DQ = QM.
⦁ Vì MQ // BD nên ![]() (so le trong).
(so le trong).
Mà ![]() (hai góc kề bù)
(hai góc kề bù)
Suy ra ![]()
Tương tự, ta có ![]()
Tam giác BCD có BC = CD và ![]() (tính chất hình thoi) nên ∆BCD là tam giác đều. Do đó
(tính chất hình thoi) nên ∆BCD là tam giác đều. Do đó ![]()
Ta có ![]()
![]()
Khi đó, ![]()
Như vậy MBNPDQ có các cạnh bằng nhau và các góc bằng nhau.
Vậy MBNPDQ là lục giác đều.
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
 Đã trả lời bởi chuyên gia
103520
Đã trả lời bởi chuyên gia
103520 -
Hỏi từ APP VIETJACK
 Đã trả lời bởi chuyên gia
68861
Đã trả lời bởi chuyên gia
68861 -
 Đã trả lời bởi chuyên gia
56682
Đã trả lời bởi chuyên gia
56682 -
 Đã trả lời bởi chuyên gia
47564
Đã trả lời bởi chuyên gia
47564 -
 Đã trả lời bởi chuyên gia
44351
Đã trả lời bởi chuyên gia
44351 -
 Đã trả lời bởi chuyên gia
36876
Đã trả lời bởi chuyên gia
36876 -
 Đã trả lời bởi chuyên gia
35387
Đã trả lời bởi chuyên gia
35387


