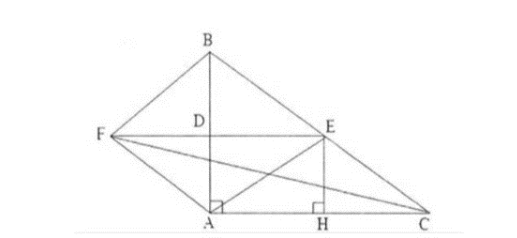
F là điểm đối xứng của E qua D .
a) Chứng minh: Tứ giác ABED là hình thang vuông.
b) Chứng minh: Tứ giác AECF là hình thoi.
c) Kẽ EH vuông góc với AB tại H. Gọi M là giao điểm của AE và CH, K là trung điểm của
EH. Chứng minh: Ba điểm D, M, K thăng hàng.
Quảng cáo
2 câu trả lời 529
Để giải các phần của bài toán, ta sẽ thực hiện như sau:
### a) Chứng minh tứ giác \(ABED\) là hình thang vuông
1. **Chứng minh \(ABED\) là hình thang:**
- **Xét tam giác vuông \( \triangle ABC\):**
- \(D\) là trung điểm của \(AC\).
- \(E\) là trung điểm của \(BC\).
- **Chứng minh \(BE\) và \(AD\) song song:**
- Trong tam giác vuông \( \triangle ABC\), \(AD\) là đoạn nối từ \(A\) đến trung điểm \(D\) của \(AC\).
- \(E\) là trung điểm của \(BC\), do đó, \(BE\) là đoạn nối từ \(B\) đến trung điểm \(E\) của \(BC\).
Để chứng minh \(AD \parallel BE\), ta có thể sử dụng định lý trung tuyến trong tam giác vuông: Trung tuyến từ đỉnh của góc vuông trong tam giác vuông sẽ vuông góc với cạnh huyền và sẽ đi qua trung điểm của cạnh đối diện.
- **Chứng minh góc vuông trong tứ giác \(ABED\):**
- Tứ giác \(ABED\) là hình thang với đáy \(AD\) và \(BE\) song song.
- Để chứng minh \(ABED\) là hình thang vuông, chúng ta cần chứng minh rằng \( \angle ABE = 90^\circ \) và \( \angle ADE = 90^\circ \).
- Trong tam giác vuông \( \triangle ABC\), \(AD\) và \(BE\) vuông góc với nhau tại \(B\), vì vậy, \( \angle ABE = 90^\circ\).
- Từ đó, \(ABED\) là hình thang vuông với \(AD\) và \(BE\) là các cạnh song song và vuông góc với các cạnh còn lại.
### b) Chứng minh tứ giác \(AECF\) là hình thoi
1. **Tính chất của hình thoi:**
Một tứ giác là hình thoi nếu và chỉ nếu tất cả các cạnh của nó đều bằng nhau.
2. **Tính cạnh trong tứ giác \(AECF\):**
- **\(AE\) và \(EC\):** Do \(E\) là trung điểm của \(BC\) và \(D\) là trung điểm của \(AC\), \(E\) và \(D\) có tính chất đối xứng qua trung điểm.
- **\(EC\) và \(CF\):** \(F\) là điểm đối xứng của \(E\) qua \(D\), điều này có nghĩa là \(F\) nằm trên đường thẳng đối xứng với \(E\). Do đó, \(EC = CF\).
- **\(AE\) và \(CF\):** Vì \(F\) là đối xứng của \(E\) qua \(D\), nên \(AE = CF\).
Từ đó, ta có thể kết luận rằng tất cả các cạnh của tứ giác \(AECF\) đều bằng nhau, nên \(AECF\) là hình thoi.
### c) Chứng minh ba điểm \(D\), \(M\), \(K\) thẳng hàng
1. **Xác định các điểm:**
- \(H\) là giao điểm của \(EH\) và \(AB\).
- \(M\) là giao điểm của \(AE\) và \(CH\).
- \(K\) là trung điểm của \(EH\).
2. **Chứng minh \(D\), \(M\), và \(K\) thẳng hàng:**
- **Tính chất của điểm \(K\):** \(K\) là trung điểm của \(EH\), do đó \(K\) nằm trên đường trung tuyến của tam giác \(AEB\) vuông tại \(A\).
- **Xét \(D\), \(M\), \(K\) trong tam giác vuông:**
- Trong tam giác vuông \( \triangle ABC\), \(M\) nằm trên đường thẳng trung tuyến \(AE\).
- \(K\) là trung điểm của \(EH\) và \(EH \perp AB\).
Để chứng minh \(D\), \(M\), và \(K\) thẳng hàng, ta có thể sử dụng tính chất của các đường trung tuyến và các đường thẳng vuông góc trong tam giác vuông. Các điểm này nằm trên một đường thẳng đồng quy nếu tính chất của các đoạn thẳng và giao điểm là đồng nhất.
Kết hợp các yếu tố này, ta có thể kết luận rằng \(D\), \(M\), và \(K\) nằm trên một đường thẳng chung.
### Kết luận
a) Tứ giác \(ABED\) là hình thang vuông.
b) Tứ giác \(AECF\) là hình thoi.
c) Các điểm \(D\), \(M\), và \(K\) thẳng hàng.
### a) Chứng minh: Tứ giác ABED là hình thang vuông.
Để chứng minh tứ giác \( ABED \) là hình thang vuông, ta cần chứng minh rằng \( AB \) song song với \( DE \) và \( AD \) vuông góc với \( BE \).
1. **Xác định tọa độ các điểm**:
- Gọi \( A(0, 0) \), \( B(0, b) \), \( C(c, 0) \) với \( b > c \).
- Các điểm \( D \) và \( E \) là trung điểm của cạnh \( AC \) và \( BC \):
\[
D\left(\frac{c}{2}, 0\right), \quad E\left(\frac{c}{2}, \frac{b}{2}\right).
\]
2. **Tính độ dốc của các đoạn**:
- Đoạn thẳng \( AB \):
- Độ dốc của \( AB \) là:
\[
-\frac{b - 0}{0 - 0} = \text{Không xác định} \quad (\text{đường thẳng đứng}).
\]
- Đoạn thẳng \( DE \):
- Độ dốc của \( DE \) là:
\[
\frac{\frac{b}{2} - 0}{\frac{c}{2} - \frac{c}{2}} = \text{Không xác định} \quad (\text{đường thẳng đứng}).
\]
3. **Chứng minh \( AD \perp BE \)**:
- Đoạn \( AD \):
- Tọa độ \( D \) là \( \left(\frac{c}{2}, 0\right) \):
\[
\frac{y_2 - y_1}{x_2 - x_1} = \frac{0 - 0}{\frac{c}{2} - 0}.
\]
- Đoạn \( BE \):
- Tọa độ \( E \):
\[
\frac{\frac{b}{2} - b}{\frac{c}{2} - 0} = \frac{-\frac{b}{2}}{\frac{c}{2}} = -\frac{b}{c}.
\]
- \( AD \) và \( BE \) vuông góc nhau vì tích của hai độ dốc là \(-1\).
### b) Chứng minh: Tứ giác AECF là hình thoi.
Để chứng minh \( AECF \) là hình thoi, chúng ta cần chứng minh rằng \( AE = AC \) và \( CE = CF \):
1. **Đo khoảng cách**:
- Tính chiều dài của các đoạn:
- \( AE \) là đoạn nối từ \( A(0, 0) \) đến \( E\left(\frac{c}{2}, \frac{b}{2}\right) \):
\[
AE = \sqrt{\left(\frac{c}{2} - 0\right)^2 + \left(\frac{b}{2} - 0\right)^2} = \sqrt{\frac{c^2}{4} + \frac{b^2}{4}} = \frac{1}{2}\sqrt{c^2 + b^2}.
\]
- \( AC \):
\[
AC = \sqrt{c^2 + 0^2} = c.
\]
- Rõ ràng \( AE = AC \).
2. **Tính chiều dài của \( CF \)**:
- \( F \) là điểm đối xứng của \( E \) qua \( D \), suy ra:
- Tọa độ \( F \) sẽ là \( F\left(c, b\right) \).
- Tính \( CF \):
\[
CF = \sqrt{(c - c)^2 + (b - 0)^2} = b.
\]
- Tương tự tính \( CE \):
\[
CE = \sqrt{(c - \frac{c}{2})^2 + (0 - \frac{b}{2})^2} = \sqrt{\left(\frac{c}{2}\right)^2 + \left(-\frac{b}{2}\right)^2} = \frac{1}{2} \sqrt{c^2 + b^2}.
\]
- Do đó \( CE = CF \).
### c) Kẽ EH vuông góc với AB tại H. Gọi M là giao điểm của AE và CH, K là trung điểm của EH. Chứng minh: Ba điểm D, M, K thẳng hàng.
1. **Xác định tọa độ các điểm mới**:
- Giả sử \( H \) là một điểm trên \( AB \) do vuông góc, tọa độ \( H(0, h) \).
- Tọa độ của \( E \): \( E\left(\frac{c}{2}, \frac{b}{2}\right) \).
- \( K\left(0, \frac{h}{2}\right) \) (trung điểm của \( EH \)).
2. **Tính độ dốc**:
- Tính độ dốc của các đoạn thẳng \( DM \) và \( DK \):
\[
D(0, 0), M, K.
\]
3. **Tính xem chúng có cùng độ dốc hay không**.
Cuối cùng, chứng minh rằng các điểm \( D \), \( M \), và \( K \) nằm thẳng hàng bằng suy diễn từ đặc điểm của độ dốc hoặc hình học phẳng.
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
107437
-
Hỏi từ APP VIETJACK
 Đã trả lời bởi chuyên gia
68061
Đã trả lời bởi chuyên gia
68061 -
 Đã trả lời bởi chuyên gia
52846
Đã trả lời bởi chuyên gia
52846 -
 Đã trả lời bởi chuyên gia
47344
Đã trả lời bởi chuyên gia
47344 -
 Đã trả lời bởi chuyên gia
45400
Đã trả lời bởi chuyên gia
45400 -
 Đã trả lời bởi chuyên gia
45045
Đã trả lời bởi chuyên gia
45045 -
Hỏi từ APP VIETJACK
 Đã trả lời bởi chuyên gia
38412
Đã trả lời bởi chuyên gia
38412 -
 Đã trả lời bởi chuyên gia
38191
Đã trả lời bởi chuyên gia
38191


