Quảng cáo
2 câu trả lời 831
Trong tam giác \( ABC \), với \( I \) là giao điểm của các tia phân giác của góc \( B \) và góc \( C \), ta có thể thực hiện những bước sau để phân tích vị trí của các điểm \( D \) và \( E \).
### Các bước thực hiện:
1. **Xác định tam giác và điểm I**:
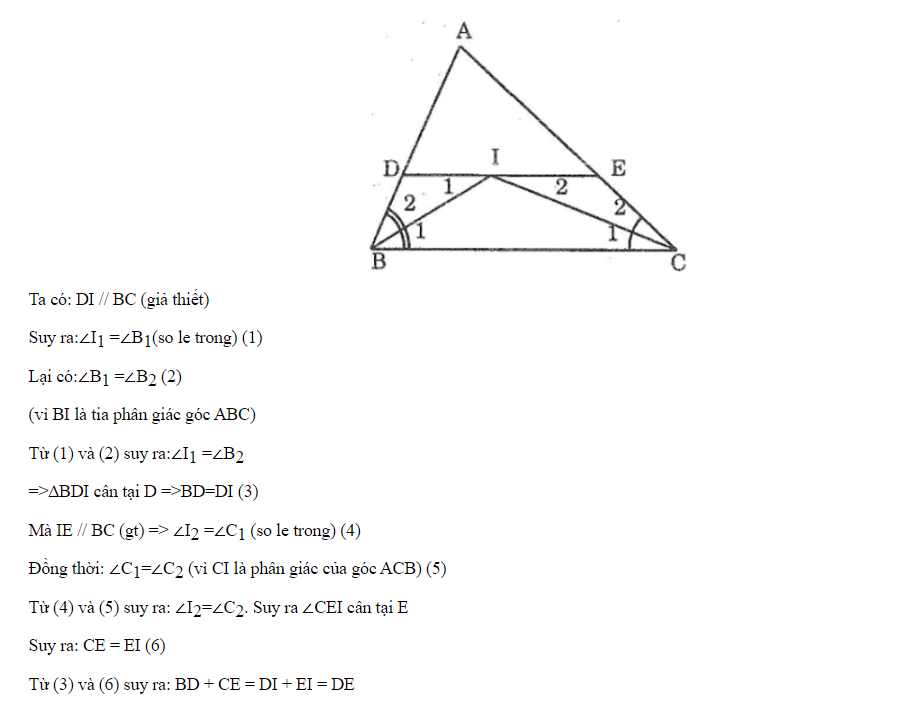
- Vẽ tam giác \( ABC \) với góc \( A \) nằm ở trên cùng, góc \( B \) nằm bên trái và góc \( C \) nằm bên phải.
- Kẻ các tia phân giác của góc \( B \) và \( C \) để xác định điểm \( I \) là điểm giao nhau của chúng (điểm trong tâm).
2. **Kẻ đường thẳng song song**:
- Từ điểm \( I \), kẻ hai đường thẳng song song với cạnh \( BC \). Những đường thẳng này sẽ cắt cạnh \( AB \) tại điểm \( D \) và cắt cạnh \( AC \) tại điểm \( E \).
### Tính chất của điểm D và E:
- Vì các đường thẳng \( DE \) song song với \( BC \), theo định lý Thales, tỷ lệ các đoạn thẳng trên hai cạnh sẽ giống nhau:
\[
\frac{AD}{DB} = \frac{AE}{EC}
\]
- Điều này có nghĩa là \( D \) và \( E \) chia các cạnh \( AB \) và \( AC \) theo cùng một tỉ lệ.
### Tính chất phối cảnh:
Khi xét vị trí của các điểm \( D \) và \( E \) trong tam giác \( ABC \), ta thấy rằng:
- Điểm \( D \) và \( E \) tạo thành hai đoạn thẳng song song với \( BC \), điều này cũng đồng nghĩa với việc \( I \) là cả một điểm trung tâm điều chỉnh cho chiều dài của các đoạn \( AD \) và \( AE \).
### Kết luận:
- Nếu bạn muốn thực hiện thuật toán hay phương pháp khác với tam giác, hoặc nếu bạn muốn tìm hiểu thêm về các tính chất của điểm \( I \) trong tam giác hoặc cách tìm tỉ lệ đoạn thẳng tương ứng, hãy cho tôi biết!
Quảng cáo
Bạn muốn hỏi bài tập?
Câu hỏi hot cùng chủ đề
-
107278
-
Hỏi từ APP VIETJACK67830
-
44998
-
38171