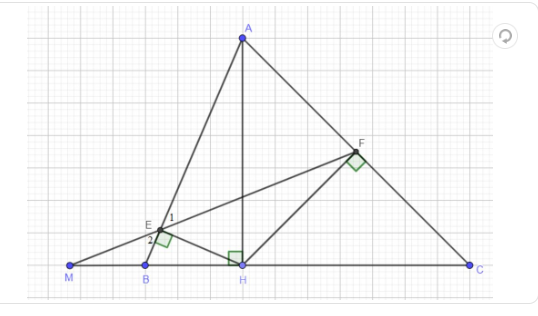
a) chứng minh ∆AEH đồng dạng ∆AHB và AE.AB=AH^2
b) đường thẳng EF cắt đường thẳng BC tại M.Chứng minh MB.MC=ME.MF
Quảng cáo
2 câu trả lời 871
Để chứng minh hai mệnh đề trong bài toán về tam giác \( \triangle ABC \), ta sẽ thực hiện theo các bước như sau.
### a) Chứng minh \(\triangle AEH \sim \triangle AHB\) và \( AE \cdot AB = AH^2 \)
1. **Chứng minh đồng dạng**:
- Xét các góc trong các tam giác:
- \(\angle AHB = 90^\circ\) (do AH là đường cao).
- \(\angle AHE = 90^\circ\) (do HE vuông góc với AB).
- \(\angle A = \angle A\) (góc chung).
Từ đó, ta có:
\[
\angle AHB = \angle AHE = 90^\circ \quad và \quad \angle A = \angle A
\]
Do đó, theo định lý về tam giác đồng dạng (góc-góc-góc):
\[
\triangle AEH \sim \triangle AHB.
\]
2. **Công thức tỉ lệ**:
Từ tính chất đồng dạng của hai tam giác, ta có:
\[
\frac{AE}{AH} = \frac{AH}{AB} \Rightarrow AE \cdot AB = AH^2.
\]
Vậy đã chứng minh được \( AE \cdot AB = AH^2 \).
### b) Chứng minh \( MB \cdot MC = ME \cdot MF \)
1. **Tình huống**:
Theo giả thiết, \(EF\) cắt \(BC\) tại \(M\).
- Gọi:
- \(MB = x\)
- \(MC = y\)
- \(ME = a\)
- \(MF = b\)
Ta cần chứng minh \(xy = ab\).
2. **Sử dụng tỉ lệ**:
Theo định lý Thales trong tam giác:
Từ hai tam giác tạo thành:
\[
\triangle AHE \sim \triangle AMB \quad và \quad \triangle AHF \sim \triangle AMC.
\]
Từ đồng dạng này, ta có:
\[
\frac{AH}{AB} = \frac{HE}{AM} \Rightarrow \frac{AH}{AB} = \frac{a}{x} \Rightarrow ax = AH \cdot AB.
\]
Tương tự:
\[
\frac{AH}{AC} = \frac{HF}{AM} \Rightarrow \frac{AH}{AC} = \frac{b}{y} \Rightarrow by = AH \cdot AC.
\]
3. **Chứng minh tỉ lệ**:
Kết hợp cả hai tỉ lệ này dẫn đến:
\[
\frac{a}{x} = \frac{b}{y} \Rightarrow xy = ab.
\]
### Kết luận
Chúng ta đã hoàn thành cả hai yêu cầu bài toán:
- Chứng minh \(\triangle AEH \sim \triangle AHB\) và \(AE \cdot AB = AH^2\).
- Chứng minh \(MB \cdot MC = ME \cdot MF\).
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
107742
-
Hỏi từ APP VIETJACK
 Đã trả lời bởi chuyên gia
68485
Đã trả lời bởi chuyên gia
68485 -
 Đã trả lời bởi chuyên gia
52942
Đã trả lời bởi chuyên gia
52942 -
 Đã trả lời bởi chuyên gia
47433
Đã trả lời bởi chuyên gia
47433 -
 Đã trả lời bởi chuyên gia
45529
Đã trả lời bởi chuyên gia
45529 -
 Đã trả lời bởi chuyên gia
45189
Đã trả lời bởi chuyên gia
45189 -
Hỏi từ APP VIETJACK
 Đã trả lời bởi chuyên gia
38558
Đã trả lời bởi chuyên gia
38558 -
 Đã trả lời bởi chuyên gia
38279
Đã trả lời bởi chuyên gia
38279