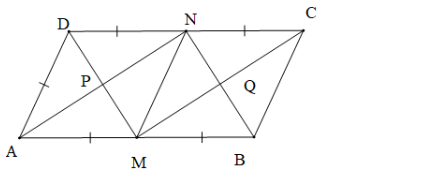
Để giải các bài toán liên quan đến tứ giác trong hình bình hành, ta có thể áp dụng các định lý và tính chất của hình bình hành.

### Phần a
**Chứng minh tứ giác \(AMCN\) là hình bình hành**

1. **Xác định các điểm:**
- \( M \) là trung điểm của \( AB \).
- \( N \) là trung điểm của \( CD \).

2. **Tính chất của trung điểm trong hình bình hành:**
- Vì \(M\) và \(N\) là trung điểm, ta có \(AM = MB\) và \(CN = ND\).

3. **Chứng minh \(AMCN\) là hình bình hành:**
- Trong hình bình hành, các cạnh đối diện bằng nhau và song song.
- Vì \(M\) và \(N\) là trung điểm của \(AB\) và \(CD\), nên \(AM = \frac{1}{2}AB\) và \(CN = \frac{1}{2}CD\). Mặt khác, \(AB\) và \(CD\) là hai cạnh đối diện của hình bình hành, nên \(AB = CD\), từ đó suy ra \(AM = CN\).

- Các đoạn thẳng \(AM\) và \(CN\) đều bằng nhau, và bởi vì \(AB\) song song với \(CD\), nên \(AM\) song song với \(CN\).

- Tương tự, xét các đoạn thẳng \(AN\) và \(MC\):
- Tứ giác \(AMCN\) có hai cặp cạnh đối diện vừa bằng nhau vừa song song (vì \(AM\) song song với \(CN\) và \(AN\) song song với \(MC\)), nên \(AMCN\) là một hình bình hành.

**Tứ giác \(AMND\) là hình gì?**

- Chúng ta có thể thấy rằng trong tứ giác \(AMND\), \(M\) và \(N\) là trung điểm của \(AB\) và \(CD\) tương ứng, và \(AD\) là cạnh của hình bình hành. Các cạnh của \(AMND\) cũng có các tính chất tương tự như hình bình hành với các cạnh đối diện bằng nhau. Ta có thể chứng minh bằng cách chỉ ra rằng các đoạn nối từ \(M\) và \(N\) tới các đỉnh đối diện cũng song song và bằng nhau. Do đó, tứ giác \(AMND\) là hình bình hành.

### Phần b
**Tứ giác \(MNIK\) là hình gì?**

- Điểm \(I\) là giao điểm của \(AN\) và \(DM\).
- Điểm \(K\) là giao điểm của \(BN\) và \(CM\).

Trong một hình bình hành, các đường chéo của nó cắt nhau tại trung điểm của chúng. Vì \(AN\) và \(DM\) đều là các đường chéo của hình bình hành \(AMND\), và \(BN\) và \(CM\) cũng là các đường chéo của hình bình hành \(ABCD\), tứ giác \(MNIK\) được tạo ra bởi giao điểm của các đường chéo này cũng là một hình bình hành.

### Phần c
**Chứng minh \(IK \parallel CD\)**

- Vì \(MNIK\) là một hình bình hành, các cặp cạnh đối diện của nó đều song song với nhau.
- Do đó, \(IK \parallel MN\) và \(MN \parallel CD\). Vậy \(IK \parallel CD\).

### Phần d
**Điều kiện để \(MINK\) là hình vuông và tính diện tích của nó**

- Tứ giác \(MINK\) là hình vuông nếu nó là hình bình hành với các góc vuông.

- Để \(MINK\) là hình vuông, các góc của nó cần phải là góc vuông. Trong một hình bình hành, nếu các cạnh đối diện bằng nhau và các góc đều bằng \(90^\circ\), thì nó là hình vuông.

- Để đảm bảo điều này trong hình bình hành \(ABCD\), ta cần các cạnh của nó phải bằng nhau (tức là \(AB = AD\) và \(BC = CD\)). Điều kiện này tương đương với hình bình hành ABCD là hình chữ nhật.

- Để tính diện tích của tứ giác \(MINK\), chúng ta cần xác định chiều dài của cạnh của nó. Do tứ giác này được tạo ra từ hình bình hành với \(AD = 4 \text{ cm}\), và các cạnh của \(MINK\) sẽ tương đương với cạnh của hình bình hành đó.

- Diện tích của tứ giác \(MINK\) khi là hình vuông bằng cạnh của nó bình phương.

- Trong hình bình hành \(ABCD\), các cạnh của tứ giác \(MINK\) đều bằng \( \frac{1}{2} \) cạnh của hình bình hành lớn hơn. Nếu \(AD = 4 \text{ cm}\), thì các cạnh của hình vuông \(MINK\) cũng có độ dài là \( \frac{1}{2} \times 4 = 2 \text{ cm}\).

- Vậy, diện tích của hình vuông \(MINK\) là \(2^2 = 4 \text{ cm}^2\).

Tóm lại:
- \(AMCN\) là hình bình hành.
- \(AMND\) cũng là hình bình hành.
- \(MNIK\) là hình bình hành.
- \(IK\) song song với \(CD\).
- Để \(MINK\) là hình vuông, hình bình hành ABCD cần là hình chữ nhật. Diện tích của hình vuông \(MINK\) là \(4 \text{ cm}^2\).

Để giải bài toán này, ta đi từng phần một.

### a. Chứng minh tứ giác AMCN là hình bình hành và xác định hình của tứ giác AMND.

**Chứng minh tứ giác AMCN là hình bình hành:**

1. Ta biết rằng M và N lần lượt là trung điểm của AB và CD.
2. Do đó, ta có:
- \( AM = MB = \frac{AB}{2} \)
- \( CN = ND = \frac{CD}{2} \)

3. Vì \( AB = 2AD \) nên ta có \( CD = AB = 2AD \). Do đó, \( CN = \frac{CD}{2} = AD \) và \( AM = AD \).

4. Trong tứ giác AMCN, ta có:
- \( AM = CN \)
- \( AN = MC \)

5. Từ đó, ta kết luận rằng tứ giác AMCN có hai cặp cạnh đối bằng nhau, nên nó là hình bình hành.

**Xác định tứ giác AMND:**

- M, N là những trung điểm của các cạnh của hình chữ nhật ABCD. Theo đó, tứ giác AMND cũng là một hình bình hành, cụ thể là hình chữ nhật (các cạnh AD và MN song song và AD vuông góc với AB).

### b. Gọi I là giao điểm của AN và DM, K là giao điểm của BN và CM. Tứ giác MNIK là hình gì?

**Chứng minh tứ giác MNIK là hình bình hành:**

- Trong tứ giác MNIK:
1. MN // IK (do M, N là trung điểm của AB và CD)
2. AN và DM giao nhau tại I, BN và CM giao nhau tại K.

Vì MN // IK và IN // MK, nên tứ giác MNIK có các cặp cạnh đối song song, do đó MNIK là hình bình hành.

### c. Ik // CD

- Vì M và N là trung điểm của các cạnh của hình bình hành (hoặc hình chữ nhật) nên IK song song với CD là đúng, bởi MN là trung điểm của AB và CD.

### d. Tìm điều kiện để tứ giác MINK là hình vuông và tính diện tích của tứ giác MINK khi AD = 4 cm.

**Điều kiện để tứ giác MINK là hình vuông:**

- Tứ giác MINK là hình vuông khi:
1. MN = NI = IK = KM (tất cả các cạnh bằng nhau).
2. Góc MNI và góc INK đều là 90 độ (các góc vuông).

- Điều kiện này xảy ra khi tứ giác ABCD là hình vuông (tức là AB = AD) và có kích thước phù hợp (góc 90 độ giữa các cạnh).

**Tính diện tích tứ giác MINK:**

1. Trong trường hợp AD = 4 cm, do đó AB = 2AD = 8 cm.
2. Từ điểm M và N đến tất cả các điểm I và K, khoảng cách đường chéo và cạnh sẽ đều bằng nhau.
3. Diện tích hình vuông MINK có công thức là:
\[
S_{MINK} = (MN)^2
\]
Với MN = AD / 2 = 4/2 = 2 cm, nên:
\[
S_{MINK} = 2^2 = 4 \text{ cm}^2.
\]

### Tóm lại:
a. Tứ giác AMCN là hình bình hành, tứ giác AMND là hình chữ nhật.
b. Tứ giác MNIK là hình bình hành.
c. IK // CD.
d. Để tứ giác MINK là hình vuông, tứ giác ABCD phải là hình vuông và diện tích MINK là 4 cm².