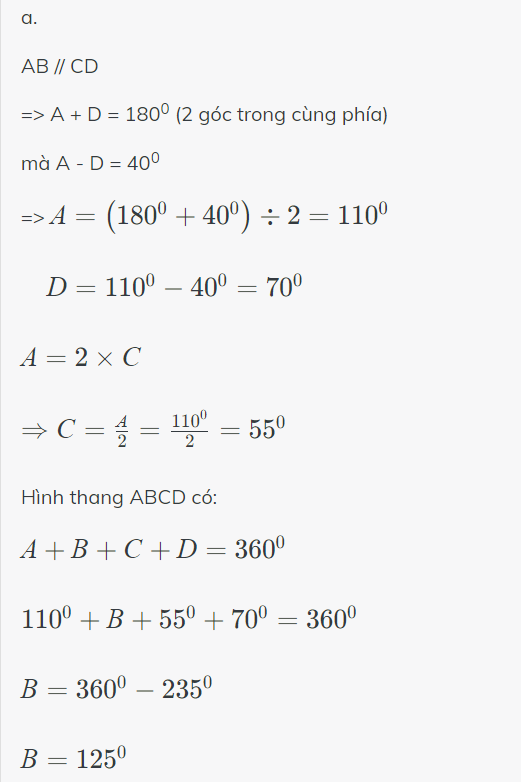Quảng cáo
2 câu trả lời 125
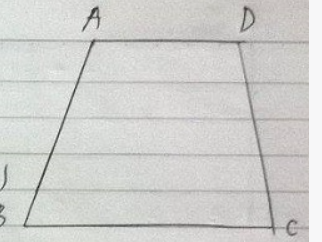
Để giải bài toán về góc của hình thang ABCD với AB // CD, ta cần dựa vào tính chất của hình thang và các thông tin đã cho:
1. **Thông tin đã cho:**
- Góc \( \angle A = 2 \angle C \)
- Góc \( \angle A - \angle D = 40^\circ \)
2. **Tính chất của hình thang:**
- Do AB và CD song song, nên:
\[ \angle A + \angle D = 180^\circ \]
\[ \angle B + \angle C = 180^\circ \]
Gọi \( \angle C = x \). Khi đó, từ thông tin \( \angle A = 2x \).
3. **Tính các góc:**
- Từ \( \angle A - \angle D = 40^\circ \), ta có:
\[ 2x - \angle D = 40^\circ \]
- Vì \( \angle A + \angle D = 180^\circ \), ta có:
\[ 2x + \angle D = 180^\circ \]
4. **Giải hệ phương trình:**
- Từ hai phương trình này, ta có:
\[
\angle D = 180^\circ - 2x \quad (1)
\]
Thay \( \angle D \) từ (1) vào phương trình \( 2x - \angle D = 40^\circ \):
\[
2x - (180^\circ - 2x) = 40^\circ
\]
\[
2x - 180^\circ + 2x = 40^\circ
\]
\[
4x - 180^\circ = 40^\circ
\]
\[
4x = 220^\circ \rightarrow x = 55^\circ
\]
- Từ đó:
\[
\angle C = x = 55^\circ
\]
\[
\angle A = 2x = 2(55^\circ) = 110^\circ
\]
5. **Tính \( \angle D \) và \( \angle B \)**:
- Tính \( \angle D \):
\[
\angle D = 180^\circ - 110^\circ = 70^\circ
\]
- Tính \( \angle B \):
\[
\angle B = 180^\circ - 55^\circ = 125^\circ
\]
6. **Kết quả**:
- Các góc của hình thang ABCD lần lượt là:
\[
\angle A = 110^\circ, \quad \angle B = 125^\circ, \quad \angle C = 55^\circ, \quad \angle D = 70^\circ
\]
Quảng cáo
Bạn muốn hỏi bài tập?
Câu hỏi hot cùng chủ đề
-
107278
-
Hỏi từ APP VIETJACK67830
-
44998
-
38171
-
우옌🖤 해영 ✨
1810 điểm
-
Sori
1745 điểm
-
사랑해요😘
1190 điểm
-
Dương Nguyễn
1140 điểm
-
`color{blue}text{HuyTùng☢`
925 điểm
-
그림 그리기를 좋아하지만, 직업이 허락하지 않아요😞
875 điểm
-
하루토 [팜 안 둥]
850 điểm
-
돈이없다 💸😭
845 điểm
-
`d.`
805 điểm
-
౨ৎ𝘉ắ𝘱ت𝘭𝘶ộ𝘤تđê⋅˚₊‧ ଳ⋆.࿔*:･🌽
785 điểm
-
🌷김은✨
630 điểm
-
Bích Hồng 625 điểm
-
누가 고철을 팔고 싶어할까요🗑️🗑️
585 điểm
-
jamJames 🥵👍
555 điểm
-
''e thik biker hơn a''
480 điểm
Rút gọn
Bài viết mới nhất Lớp 8
-
3 năm trước8220
-
3 năm trước7732
-
3 năm trước6571
-
3 năm trước6459
-
3 năm trước6291
