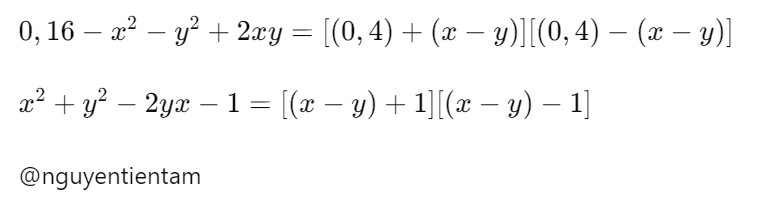0,16 - x2 - y2 + 2xy; x2 + y2 - 2yx - 1.phân tích đt thành nhân tử

Nguyen Vu Thi Hỏi từ APP VIETJACK

đã hỏi trong Lớp 8 Toán học

· 11:52 01/08/2024

0,16 - x²- y²+ 2xy; x²+ y²- 2yx - 1.phân tích đt thành nhân tử

Hỏi chi tiết

Quảng cáo

1 năm trước

Để phân tích các đa thức thành nhân tử, chúng ta sẽ xem xét hai biểu thức sau:

1. \(0.16 - x^2 - y^2 + 2xy\)
2. \(x^2 + y^2 - 2yx - 1\)

### Biểu thức 1: \(0.16 - x^2 - y^2 + 2xy\)

Trước tiên, hãy xem xét cách biểu thức này có thể được viết lại. Chúng ta biết rằng \(2xy = 2xy\), do đó:

\[0.16 - x^2 - y^2 + 2xy = 0.16 - (x^2 - 2xy + y^2)\]

Ta nhận thấy rằng \(x^2 - 2xy + y^2\) là bình phương của \((x-y)\):

\[0.16 - (x-y)^2\]

Chúng ta có thể viết lại biểu thức dưới dạng hiệu của hai bình phương:

\[0.16 - (x-y)^2 = (0.4)^2 - (x-y)^2\]

Sử dụng công thức hiệu của hai bình phương \(a^2 - b^2 = (a - b)(a + b)\):

\[(0.4)^2 - (x-y)^2 = (0.4 - (x-y))(0.4 + (x-y))\]

Vậy, biểu thức đầu tiên phân tích thành:

\[0.16 - x^2 - y^2 + 2xy = (0.4 - x + y)(0.4 + x - y)\]

### Biểu thức 2: \(x^2 + y^2 - 2yx - 1\)

Ta nhận thấy rằng \(x^2 + y^2 - 2yx\) là bình phương của \((x-y)\):

\[x^2 + y^2 - 2yx - 1 = (x-y)^2 - 1\]

Sử dụng công thức hiệu của hai bình phương \(a^2 - b^2 = (a - b)(a + b)\):

\[(x-y)^2 - 1 = (x-y - 1)(x-y + 1)\]

Vậy, biểu thức thứ hai phân tích thành:

\[x^2 + y^2 - 2yx - 1 = (x-y-1)(x-y+1)\]

### Tóm tắt:

1. \(0.16 - x^2 - y^2 + 2xy\) phân tích thành \((0.4 - x + y)(0.4 + x - y)\).
2. \(x^2 + y^2 - 2yx - 1\) phân tích thành \((x-y-1)(x-y+1)\).

...Xem thêm

0 bình luận

Đăng nhập để hỏi chi tiết

1 năm trước

Chúc bạn học vui!

0 bình luận

Đăng nhập để hỏi chi tiết

Quảng cáo

Bạn muốn hỏi bài tập?