Để chứng minh rằng \( aefd \) là hình bình hành và \( aecf \) là hình bình hành, ta sẽ dùng các tính chất của hình bình hành và tính chất của trung điểm.

1. **Chứng minh \( aefd \) là hình bình hành:**
- \( e \) và \( f \) trung điểm của cạnh \( ab \) và \( cd \) tương ứng.
- Do đó, ta có:
- \( ae = eb \)
- \( cf = fd \)

- Chứng minh \( ae \parallel df \) và \( af \parallel ed \):
- Vì \( ab \parallel cd \) (tính chất của hình bình hành), nên đoạn thẳng \( ef \) cũng sẽ song song với các đoạn còn lại do \( e \) \( f \) là trung điểm của \( ab \) và \( cd \).
- Từ đó có \( ae \parallel df \) và \( af \parallel ed \).

- Cuối cùng, vì \( ae = ef \) và \( cf = ed \), ta có hai cặp cạnh đối diện trong tứ giác \( aefd \) là bằng nhau và song song, nên \( aefd \) là hình bình hành.

2. **Chứng minh \( aecf \) là hình bình hành:**
- \( ae \) là đoạn nối từ đỉnh \( a \) đến trung điểm \( e \) của \( ab \), \( cf \) là đoạn nối từ điểm trung điểm \( f \) của \( cd \).
- Tương tự, ta chứng minh \( ae \parallel cf \) và \( ac \parallel ef \):
- Từ tính chất \( ab \parallel cd \), \( ae \parallel cf \) do \( e \) và \( f \) là trung điểm, cho nên \( ae \parallel cf \).
- Các đoạn \( ac \) và \( ef \) cũng sẽ song song vì hai đoạn này đều nằm trên một đường thẳng chung và \( e, f \) là trung điểm.

- Cuối cùng, hai cặp cạnh đối diện \( ae = cf \) và \( ac = ef \) đều bằng nhau, do đó \( aecf \) cũng là hình bình hành.

**Kết luận:** Chúng ta đã chứng minh rằng \( aefd \) và \( aecf \) đều là hình bình hành dựa trên tính chất của các cạnh và đoạn thẳng song song.

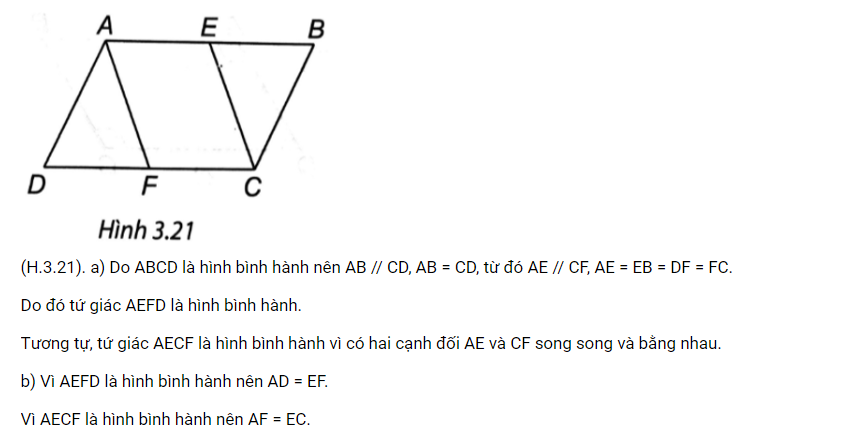
Để chứng minh các tính chất của hình bình hành ABCD với E và F là trung điểm của AB và CD, chúng ta có thể làm như sau:

Chứng minh AEFD là hình bình hành:

Vì ABCD là hình bình hành nên AB // CD và AB = CD.
E và F lần lượt là trung điểm của AB và CD nên AE = EB và CF = FD.
Do đó, AE // DF và AE = DF.
Tứ giác AEFD có hai cặp cạnh đối song song và bằng nhau nên AEFD là hình bình hành.
Chứng minh AECF là hình bình hành:

Vì ABCD là hình bình hành nên AD // BC và AD = BC.
E và F lần lượt là trung điểm của AB và CD nên AE = EB và CF = FD.
Do đó, AE // CF và AE = CF.
Tứ giác AECF có hai cặp cạnh đối song song và bằng nhau nên AECF là hình bình hành.
Chứng minh EF = AD:

Vì E và F là trung điểm của AB và CD nên EF là đường trung bình của tam giác ABC và tam giác ADC.
Do đó, EF // AD và EF = 1/2 AD.
Vì ABCD là hình bình hành nên AD = BC.
Do đó, EF = AD.
Chứng minh AF = DC:

Vì AEFD là hình bình hành nên AF = ED.
Vì ABCD là hình bình hành nên AB = CD.
Do đó, AF = DC.