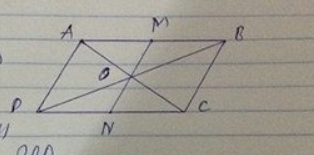
a. Chứng minh tứ giác \( AMCN \) là hình bình hành

1. **Xác định các điểm và đoạn thẳng:**
- \( M \) là trung điểm của \( AB \).
- \( N \) là trung điểm của \( DC \).

2. **Tính chất của đoạn thẳng \( MN \):**
- Vì \( M \) và \( N \) là trung điểm của các đoạn đối diện \( AB \) và \( DC \) trong hình bình hành, đoạn thẳng \( MN \) nối hai trung điểm này sẽ song song và bằng đoạn đối diện của hình bình hành \( AC \) (theo định lý trung điểm trong hình bình hành).

3. **Chứng minh các đoạn thẳng đối diện bằng nhau:**
- Trong hình bình hành, các đoạn thẳng nối các trung điểm của các cạnh đối diện là song song và bằng nhau. Do đó, \( AM \parallel NC \) và \( AM = NC \). Tương tự, \( MN \parallel AC \) và \( MN = AC \).

4. **Chứng minh \( AMCN \) là hình bình hành:**
- Tứ giác \( AMCN \) có các cạnh đối diện song song và bằng nhau, do đó nó thỏa mãn điều kiện của một hình bình hành.

### b. Chứng minh tứ giác \( BMDN \) là hình bình hành

1. **Xác định các điểm và đoạn thẳng:**
- \( M \) là trung điểm của \( AB \).
- \( N \) là trung điểm của \( DC \).
- \( B \) và \( D \) là các đỉnh của hình bình hành.

2. **Chứng minh các đoạn thẳng đối diện bằng nhau:**
- Vì \( M \) và \( N \) là các trung điểm của \( AB \) và \( DC \), nên \( MN \) song song và bằng nhau với \( BD \) (theo định lý trung điểm của hình bình hành).

- Các đoạn nối từ \( B \) đến \( M \) và từ \( D \) đến \( N \) là các đoạn nối từ đỉnh đến các trung điểm của các đoạn đối diện. Do đó, \( BM = DN \).

3. **Chứng minh các đoạn thẳng đối diện song song:**
- Đoạn thẳng \( MN \) song song với \( BD \), và \( BM \parallel DN \), đồng thời \( BM = DN \).

4. **Chứng minh \( BMDN \) là hình bình hành:**
- Tứ giác \( BMDN \) có các cạnh đối diện song song và bằng nhau, do đó nó thỏa mãn điều kiện của một hình bình hành.

**Kết luận:**

- Tứ giác \( AMCN \) là hình bình hành vì các cạnh đối diện của nó song song và bằng nhau.
- Tứ giác \( BMDN \) là hình bình hành vì các cạnh đối diện của nó cũng song song và bằng nhau.

Để chứng minh các yêu cầu trong bài toán về hình bình hành \( ABCD \) với \( M \) là trung điểm của \( AB \) và \( N \) là trung điểm của \( CD \), ta sẽ thực hiện từng phần như sau:

### a. Chứng minh \( AMCN \) là hình bình hành

1. **Thiết lập:**
- Ta có hình bình hành \( ABCD \) với \( M \) là trung điểm của \( AB \) (tức là \( AM = MB \)) và \( N \) là trung điểm của \( CD \) (tức là \( CN = ND \)).

2. **Chứng minh:**
- Vì \( ABCD \) là hình bình hành, ta có \( AB \parallel CD \) và \( AD \parallel BC \).
- Do \( M \) là trung điểm của \( AB \) và \( N \) là trung điểm của \( CD \), theo tính chất của hình bình hành, ta có:
- \( AB \parallel CD \Rightarrow AM \parallel CN \) (do cùng nằm trên các đoạn thẳng song song)
- \( AM = MB \) và \( CN = ND \)

- Kết luận:
- Tứ giác \( AMCN \) có:
- \( AM \parallel CN \) và \( AM = CN \).
- \( AN \parallel MC \) (do \( AD \parallel BC \)).
- Vì vậy, theo định nghĩa, \( tứ giác AMCN \) có cặp cạnh đối diện bằng nhau và song song, nên \( AMCN \) là hình bình hành.

### b. Chứng minh \( BMDN \) là hình bình hành

1. **Thiết lập:**
- Tương tự, ta có \( M \) là trung điểm của \( AB \) và \( N \) là trung điểm của \( CD \).

2. **Chứng minh:**
- Từ hình bình hành \( ABCD \), ta biết rằng \( AD \parallel BC \).
- Vì \( M \) là trung điểm của \( AB \) và \( N \) là trung điểm của \( CD \), ta có:
- \( BM \parallel DN \) (do \( AB \parallel CD \)).
- \( BM = AM \) (từ \( M \) là trung điểm của \( AB \) và \( AM = MB \)).
- \( DN = CN \) (từ \( N \) là trung điểm của \( CD \) và \( CN = ND \)).

- Kết luận:
- Tứ giác \( BMDN \) có:
- \( BM \parallel DN \) và \( BM = DN \).
- \( BD \parallel MN \) và các đoạn \( BN \, và \, DM \) có độ dài bằng nhau.
- Do đó, ta có \( BMDN \) là hình bình hành.

### Tóm tắt:
1. Tứ giác \( AMCN \) là hình bình hành.
2. Tứ giác \( BMDN \) là hình bình hành.

Nếu bạn cần thêm sự giải thích hoặc có câu hỏi khác, xin hãy cho tôi biết!