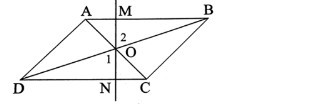
Để giải bài toán này, ta cần sử dụng một số tính chất cơ bản của hình bình hành và tam giác. Dưới đây là các bước chứng minh:

### a. Chứng minh tam giác \( OAM \) đồng dạng với tam giác \( OCN \)

1. **Cơ sở chứng minh:**

- Hình bình hành có 2 đường chéo cắt nhau tại trung điểm của chúng. Do đó, \( O \) là trung điểm của cả hai đường chéo \( AC \) và \( BD \).

- Các cạnh đối diện của hình bình hành bằng nhau và các góc đối diện bằng nhau.

2. **Chứng minh đồng dạng:**

- **Góc \( \angle OAM \) và \( \angle OCN \):**
- Vì \( O \) là trung điểm của đường chéo \( AC \), góc \( \angle OAM \) là góc giữa đường chéo \( AC \) và đường thẳng \( AM \).
- Tương tự, góc \( \angle OCN \) là góc giữa đường chéo \( BD \) và đường thẳng \( CN \).

- **Góc \( \angle OMA \) và \( \angle ONC \):**
- Các góc này bằng nhau vì đường chéo của hình bình hành chia nhau thành các góc bằng nhau (hình bình hành có góc chéo đối diện bằng nhau).

- **Tỉ lệ cạnh tương ứng:**
- Do \( \triangle OAM \) và \( \triangle OCN \) có cùng góc tại \( O \) và các góc đối diện của hình bình hành bằng nhau, nên tỉ lệ các cạnh tương ứng cũng bằng nhau.

Do đó, theo tiêu chuẩn góc-góc-góc (góc-góc-góc), ta có \( \triangle OAM \sim \triangle OCN \).

### b. Chứng minh tứ giác \( MBND \) là hình bình hành

1. **Các đoạn thẳng đối diện bằng nhau:**

- Trong một hình bình hành, các cạnh đối diện bằng nhau. Do đó, các cạnh đối diện của tứ giác \( MBND \) phải bằng nhau.

2. **Góc đối diện bằng nhau:**

- Từ việc \( \triangle OAM \sim \triangle OCN \), ta có \( \angle OMA = \angle ONC \) và \( \angle OAM = \angle OCN \). Do đó, các góc trong tứ giác \( MBND \) cũng phải bằng nhau.

3. **Các đoạn thẳng cắt nhau tại trung điểm:**

- Các đường chéo của hình bình hành chia nhau tại trung điểm. Do đó, trong tứ giác \( MBND \), các đoạn nối từ \( M \) đến \( N \) và từ \( B \) đến \( D \) sẽ cắt nhau tại trung điểm của nhau, đảm bảo rằng tứ giác \( MBND \) thỏa mãn tính chất của hình bình hành.

Do đó, tứ giác \( MBND \) là hình bình hành.

**Kết luận:**

- Ta đã chứng minh rằng \( \triangle OAM \) đồng dạng với \( \triangle OCN \) và tứ giác \( MBND \) là hình bình hành dựa trên các tính chất của hình bình hành và các góc của các tam giác.

Để chứng minh các yêu cầu trong bài toán về hình bình hành với hai đường chéo cắt nhau tại điểm \( O \), ta làm như sau:

### a. Chứng minh tam giác \( OAM \) = tam giác \( OCN \)

1. **Cách tiếp cận:**
- Xét hình bình hành \( ABCD \) với \( O \) là giao điểm của hai đường chéo \( AC \) và \( BD \).
- Theo tính chất của hình bình hành, ta có \( AB \parallel CD \) và \( AD \parallel BC \).

2. **Chi tiết chứng minh:**
- Ta có \( OA = OC \) (vì \( O \) là giao điểm của đường chéo trong hình bình hành).
- \( OM \) và \( ON \) là đường thẳng cắt \( AB \) và \( CD \) tại \( M \) và \( N \).
- Do \( AB \parallel CD \), nên các góc \( \angle OMA \) và \( \angle ONC \) là các góc đồng vị.
- Vậy \( \angle OAM = \angle OCN \).

Từ đó, ta có thể kết luận:

- Tam giác \( OAM \) và tam giác \( OCN \) có:
- \( OA = OC \)
- \( OM = ON \) (do cùng nằm trên đường thẳng cắt \( AB \) và \( CD \))
- \( \angle OAM = \angle OCN \)

- Theo tiêu chí \( \text{Cạnh-Cạnh-Cạnh} (CCC) \), ta có:

\[
\triangle OAM \cong \triangle OCN
\]

### b. Chứng minh tứ giác \( MBND \) là hình bình hành

1. **Điều kiện hình bình hành:**
- Để chứng minh \( MBND \) là hình bình hành, ta cần chứng minh hai cặp cạnh đối diện của nó bằng nhau.

2. **Chứng minh:**
- Từ \( \triangle OAM \cong \triangle OCN \), ta có:
- \( OA = OC \) (cạnh)
- \( OM = ON \) (cạnh)
- \( \angle OAM = \angle OCN \) (góc)

- Từ điều này, ta thấy rằng \( AM = CN \).

- Tiếp theo, vì \( AB \parallel CD \) và \( AD \parallel BC \), do đó:
- \( MB \) song song với \( ND \) và cùng dài \( MN \).

- Kết luận:
- Tứ giác \( MBND \) có \( MB \parallel ND \) và \( MN \parallel BD \),
- Và \( MB = ND \), nên theo định nghĩa:

\[
MBND \text{ là hình bình hành.}
\]

### Tóm lại:
1. Tam giác \( OAM \) và tam giác \( OCN \) là hai tam giác bằng nhau.
2. Tứ giác \( MBND \) là hình bình hành.

Hy vọng các bước chứng minh trên hữu ích cho bạn! Nếu bạn cần thêm thông tin, hãy cho tôi biết!