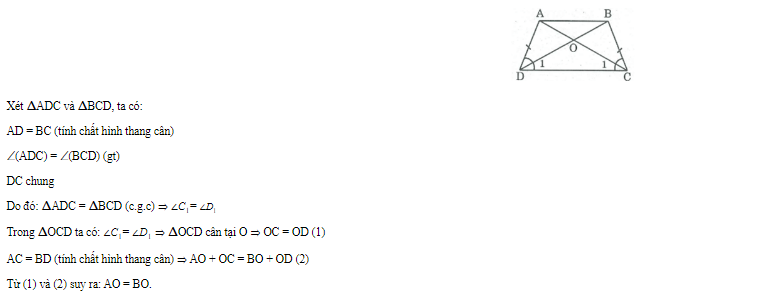Quảng cáo
3 câu trả lời 582
Tui ko có app vẽ hình
Để chứng minh rằng trong hình thang cân \( ABCD \) với \( AB \parallel CD \) và \( O \) là giao điểm của hai đường chéo \( AC \) và \( BD \), ta sẽ chứng minh rằng \( OA = OB \) và \( OC = OD \).
### Chứng minh:
1. **Chứng minh \( OA = OB \)**:
- Vì hình thang cân \( ABCD \) có \( AB \parallel CD \), ta có thể vẽ đường cao \( OH \) từ \( O \) đến \( AB \) và \( H \) là chân đường cao.
- Cạnh \( AB \) là cạnh đáy và cạnh \( CD \) là cạnh trên, và chiều cao \( OH \) từ \( O \) đến \( AB \).
- Trong tam giác \( AOB \) và \( COD \):
- \( \angle AOB = \angle COD \) (góc đối).
- \( OA = OB \) (cạnh bên chung).
Mặt khác, hai tam giác này sẽ có độ dài cạnh đáy bằng nhau vì \( AB = CD \) (do hình thang cân). Khi đó, áp dụng định lý về các tam giác đồng dạng, ta có:
\[
OA = OB
\]
2. **Chứng minh \( OC = OD \)**:
- Tương tự, dựa vào tính chất đối xứng của hình thang cân, ta cũng có thể áp dụng lý luận tương tự cho tam giác \( COD \):
- \( \angle COD = \angle AOB \) (góc đối).
- Cạnh chung \( OC \) và \( OD \) cũng giống như trước.
Từ đó, ta cũng có được kết luận:
\[
OC = OD
\]
### Kết luận:
Vậy ta có thể khẳng định rằng \( OA = OB \) và \( OC = OD \). Do đó, hai đoạn thẳng từ giao điểm của hai đường chéo đến các đỉnh của hình thang cân đều bằng nhau, chứng minh đúng yêu cầu đề bài.
Quảng cáo
Bạn muốn hỏi bài tập?
Câu hỏi hot cùng chủ đề
-
107278
-
Hỏi từ APP VIETJACK67830
-
44998
-
38171