2.cho hình chóp tam giác đều có thể tích =30cm3,chiều cao =12cm.tính diện tích đáy hình chóp đó
giúp mình 2 bài này với mn ơiii
Quảng cáo
3 câu trả lời 418
1.
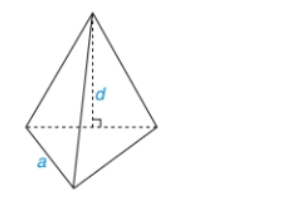
Chu vi đáy là:
8*4=32(cm)
Diện tích xung quanh là:
32⋅12=384(cm2)
2.

### 1. Tính diện tích xung quanh (SXQ) của hình chóp tam giác đều.
**Thông tin đã cho:**
- Cạnh đáy (a) = 8 cm
- Trung đoạn (l) = 12 cm
**Diện tích xung quanh (SXQ)** của hình chóp tam giác đều được tính theo công thức:
\[
S_{xq} = \frac{1}{2} \times P_{đáy} \times l
\]
Trong đó \( P_{đáy} \) là chu vi của đáy.
**Bước 1: Tính chu vi của đáy (P đáy)**
- Đáy là tam giác đều, do đó chu vi của nó sẽ là:
\[
P_{đáy} = 3 \times a = 3 \times 8 = 24 \text{ cm}
\]
**Bước 2: Tính diện tích xung quanh (SXQ)**
\[
S_{xq} = \frac{1}{2} \times P_{đáy} \times l = \frac{1}{2} \times 24 \times 12 = 144 \text{ cm}^2
\]
### **Kết luận:**
- Diện tích xung quanh (SXQ) của hình chóp tam giác đều là **144 cm²**.
---
### 2. Tính diện tích đáy của hình chóp tam giác đều.
**Thông tin đã cho:**
- Thể tích (V) = 30 cm³
- Chiều cao (h) = 12 cm
**Công thức tính thể tích của hình chóp** là:
\[
V = \frac{1}{3} \times S_{đáy} \times h
\]
**Bước 1: Thay số vào công thức và tính diện tích đáy (S đáy)**
\[
30 = \frac{1}{3} \times S_{đáy} \times 12
\]
**Bước 2: Giải phương trình để tìm \( S_{đáy} \)**
\[
30 = 4 \times S_{đáy} \\
S_{đáy} = \frac{30}{4} = 7.5 \text{ cm}^2
\]
### **Kết luận:**
- Diện tích đáy của hình chóp tam giác đều là **7.5 cm²**.
Chắc chắn rồi! Hãy cùng giải quyết từng bài toán một nhé.
Bài 1: Tính diện tích xung quanh của hình chóp tam giác đều
Dữ liệu:
Cạnh đáy ( a = 8 ) cm
Trung đoạn (đường cao từ đỉnh xuống trung điểm của cạnh đáy) ( h = 12 ) cm
Giải:
Tính chiều cao của tam giác đều đáy: [ h_{\text{đáy}} = \frac{a \sqrt{3}}{2} = \frac{8 \sqrt{3}}{2} = 4 \sqrt{3} , \text{cm} ]
Tính chiều cao của mỗi mặt bên tam giác cân: Sử dụng định lý Pythagore trong tam giác vuông với cạnh đáy là ( 4 ) cm (nửa cạnh đáy) và trung đoạn là ( 12 ) cm: [ h_{\text{mặt bên}} = \sqrt{12^2 + 4^2} = \sqrt{144 + 16} = \sqrt{160} = 4 \sqrt{10} , \text{cm} ]
Tính diện tích một mặt bên: [ S_{\text{mặt bên}} = \frac{1}{2} \times a \times h_{\text{mặt bên}} = \frac{1}{2} \times 8 \times 4 \sqrt{10} = 16 \sqrt{10} , \text{cm}^2 ]
Tính diện tích xung quanh của hình chóp: [ S_{\text{xq}} = 3 \times S_{\text{mặt bên}} = 3 \times 16 \sqrt{10} = 48 \sqrt{10} , \text{cm}^2 ]
Bài 2: Tính diện tích đáy của hình chóp tam giác đều
Dữ liệu:
Thể tích ( V = 30 ) cm³
Chiều cao ( h = 12 ) cm
Giải:
Sử dụng công thức thể tích hình chóp: [ V = \frac{1}{3} \times S_{\text{đáy}} \times h ]
Tính diện tích đáy: [ 30 = \frac{1}{3} \times S_{\text{đáy}} \times 12 ] [ S_{\text{đáy}} = \frac{30 \times 3}{12} = \frac{90}{12} = 7.5 , \text{cm}^2 ]
Hy vọng các bước trên giúp bạn hiểu rõ hơn về cách giải hai bài toán này! Nếu bạn có bất kỳ câu hỏi nào khác, đừng ngần ngại hỏi nhé!
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
107593
-
Hỏi từ APP VIETJACK
 Đã trả lời bởi chuyên gia
68300
Đã trả lời bởi chuyên gia
68300 -
 Đã trả lời bởi chuyên gia
52884
Đã trả lời bởi chuyên gia
52884 -
 Đã trả lời bởi chuyên gia
47390
Đã trả lời bởi chuyên gia
47390 -
 Đã trả lời bởi chuyên gia
45461
Đã trả lời bởi chuyên gia
45461 -
 Đã trả lời bởi chuyên gia
45109
Đã trả lời bởi chuyên gia
45109 -
Hỏi từ APP VIETJACK
 Đã trả lời bởi chuyên gia
38488
Đã trả lời bởi chuyên gia
38488 -
 Đã trả lời bởi chuyên gia
38230
Đã trả lời bởi chuyên gia
38230


