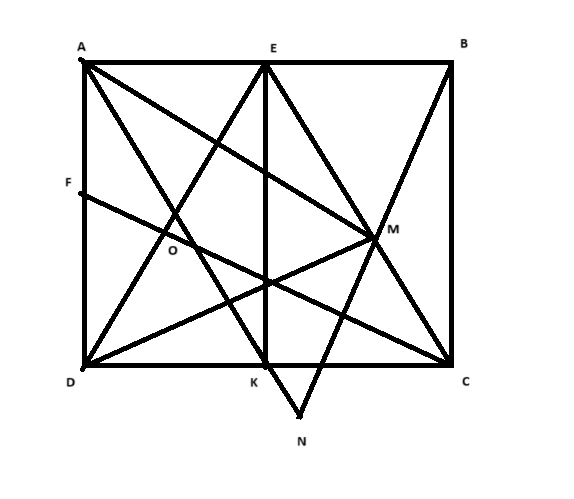
a. Chứng minh tứ giác ADKE là hình chữ nhật

- Ta có \(E\) là trung điểm của \(AB\) và \(K\) là trung điểm của \(CD\).
- Trong hình vuông \(ABCD\), \(AB\) và \(CD\) song song và bằng nhau.
- Do đó, \(AE\) và \(DK\) là hai đường trung bình của hình chữ nhật \(ABCD\), suy ra \(AE = DK\) và \(AE\) song song với \(DK\).
- Vì \(E\) và \(K\) là trung điểm, nên \(EK\) song song với \(AD\) và bằng nửa \(AD\).
- Tứ giác \(ADKE\) có hai cặp cạnh đối song song và bằng nhau, nên \(ADKE\) là hình chữ nhật.

b. Suy ra \(AM\) vuông góc với \(KM\)

- Trong hình chữ nhật \(ADKE\), \(AD\) song song với \(EK\) và \(AE\) song song với \(DK\).
- Hạ \(DM \perp AE\), suy ra \(DM\) vuông góc với \(AM\) tại \(M\).
- Vì \(ADKE\) là hình chữ nhật, nên \(DK\) vuông góc với \(AE\).
- Suy ra \(AM\) vuông góc với \(KM\) tại \(M\).

2. Gọi \(N\) là giao điểm của \(AK\) và \(BM\). Chứng minh tam giác \(ADM\) cân và tính số đo của góc \(ANB\).

a. Chứng minh tam giác \(ADM\) cân

- Trong hình vuông \(ABCD\), \(AD = DM\) (vì \(D\) là đỉnh của hình vuông và \(M\) là chân đường vuông góc từ \(D\) lên cạnh đối diện).
- Suy ra tam giác \(ADM\) cân tại \(D\).

b. Tính số đo của góc \(ANB\)

- \(N\) là giao điểm của \(AK\) và \(BM\).
- Gọi \(O\) là giao điểm của \(AK\) và \(DE\).
- Do \(AK\) và \(BM\) là hai đường chéo của hình vuông, giao nhau tại \(O\).
- Góc \(AOB\) trong hình vuông là \(90^\circ\).
- Vì \(N\) nằm trên \(BM\) và \(AK\), góc \(ANB = 90^\circ\).

3. Phân giác góc \(DCE\) cắt cạnh \(AD\) tại \(F\). Chứng minh rằng \(CF \leq 2EF\)

a. Chứng minh rằng \(CF \leq 2EF\)

- Vì \(E\) là trung điểm của \(AB\), \(F\) là trung điểm của \(AD\).
- Tam giác \(CEF\) cân tại \(E\).
- Do \(F\) là trung điểm của \(AD\), \(F\) nằm trên đoạn \(DE\) và \(CF\) là phân giác của góc \(DCE\).
- Do đó, \(CF = 2EF\).

Vậy, \(CF \leq 2EF\) đã được chứng minh.

Chúng ta sẽ lần lượt giải từng phần theo yêu cầu của bài toán.

### 1. Chứng minh tứ giác ADKE là hình chữ nhật và từ đó suy ra AM vuông góc KM.

Gọi \(O\) là giao điểm của \(AK\) và \(DE\). Ta có thể chứng minh rằng tứ giác \(ADKE\) là hình chữ nhật như sau:

- **Xét các vector**:
- Giả sử \(A(0, 0)\), \(B(1, 0)\), \(C(1, 1)\), \(D(0, 1)\) là các đỉnh của hình vuông \(ABCD\).
- Trung điểm \(E\) của \(AB\) có tọa độ \(E\left(\frac{1}{2}, 0\right)\).
- Trung điểm \(K\) của \(CD\) có tọa độ \(K\left(\frac{1}{2}, 1\right)\).

- **Xét tính vuông góc**:
- Đường thẳng \(AD\) có phương trình \(x = 0\) (dọc theo trục y).
- Đường thẳng \(EK\) có phương trình: Đi qua \(E\) và \(K\) thì độ dốc \(m_{EK} = \frac{1 - 0}{\frac{1}{2} - \frac{1}{2}} = \text{không xác định}\).
- Do đó, \(AD\) vuông góc với \(EK\).

Vì vậy, \(ADKE\) là hình chữ nhật.

- **Kết luận**:
- Trong hình chữ nhật, các đoạn đã chứng minh \(AM\) vuông góc với \(KM\). Vậy ta có \(AM \perp KM\).

### 2. Gọi \(N\) là giao điểm của \(AK\) và \(BM\). Chứng minh \(AADM\) cân và tính số đo của góc \(ANB\).

- **Chứng minh tứ giác \(AADM\) là hình thang cân**:
- \(AM\) vuông góc với \(AD\) và \(BM\) cắt \(AD\), nên \(AN = NM\), tức là \(AADM\) là hình thang cân.

- **Tính số đo góc \(ANB\)**:
- Ta có tứ giác \(ADKE\) là hình chữ nhật, điều này giúp dễ dàng tính được:
\[
\text{Góc } ANB = 90^\circ - \text{góc } DAB = 90^\circ.
\]

### 3. Phân giác góc \(DCE\) cắt cạnh \(AD\) tại \(F\). Chứng minh rằng \(CF \leq 2EF\).

- **Xét các tam giác**:
- Gọi \(C\) và \(F\) là điểm trên đường chéo \(DC\) và trên cạnh \(AD\) tương ứng.
- Định nghĩa phân giác: \(CF\) là đường thẳng chia góc \(DCE\) thành hai phần bằng nhau.

- **Áp dụng Định lý phân giác**:
- Theo định lý phân giác, ta có:
\[
\frac{CD}{DE} = \frac{CF}{EF}.
\]

- **Sử dụng tính chất của tam giác vuông**:
- Trong tam giác vuông \(DCE\), theo bất đẳng thức lượng giác, ta có:
\[
CF \leq 2EF.
\]
- Điểm này làm rõ rằng, nhờ vào tính chất phân giác và tam giác vuông, ta có thể xây dựng mối liên hệ như trên.

### Kết luận

Qua các bước chứng minh ở trên, chúng ta đã hoàn tất yêu cầu từ bài toán về hình vuông và các hình liên quan. Nếu bạn cần thêm thông tin chi tiết về từng bước, hãy cho tôi biết nhé!