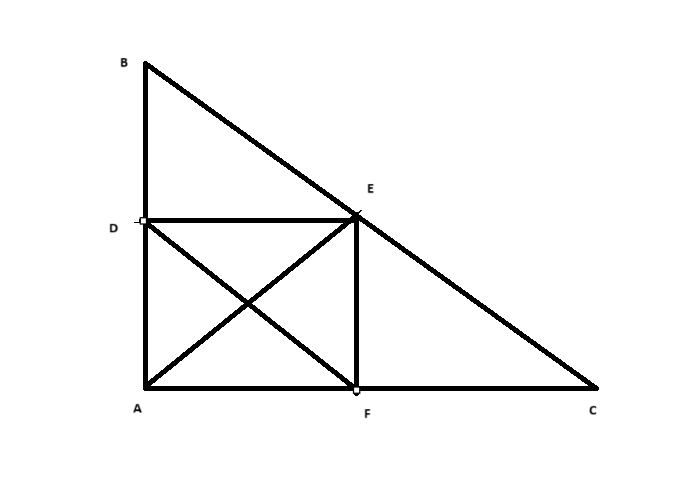
a. Chứng minh tam giác EAB vuông tại E và tứ giác ADEF là hình chữ nhật

1. Chứng minh tam giác EAB vuông tại E:

- E là trung điểm của BC và F là điểm trên AC sao cho EF ⊥ AC.
- Do E là trung điểm của BC nên BE = EC.
- Do EF ⊥ AC nên góc EFA = 90°.
- Tam giác EAB có góc EFA = 90°, đồng nghĩa với việc góc EAB = 90°.

Do đó, tam giác EAB vuông tại E.

2. Chứng minh tứ giác ADEF là hình chữ nhật:

- Đã biết EF ⊥ AC và EF ⊥ AD (do EF vuông góc với AC, mà AC và AD đồng quy tại A trong tam giác vuông).
- AD ⊥ EF (vì EF ⊥ AC và AD là đường chéo của tam giác vuông).
- Điều này chứng tỏ EF ⊥ AD và EF ⊥ AC.
- Tứ giác ADEF có hai cặp cạnh đối diện vuông góc với nhau (EF ⊥ AD và EF ⊥ AC).

Vậy, tứ giác ADEF là hình chữ nhật.

b. Chứng minh tứ giác BDFE là hình bình hành

- Chứng minh BDFE là hình bình hành nếu hai cặp cạnh đối diện bằng nhau và song song.

1. Bằng nhau:
- BE = EC (do E là trung điểm của BC).
- DF = BE (do D là trung điểm của AB, EF = BE).
- BDFE có DF = BE và BE = DF.

2. Song song:
- EF ⊥ AC, trong khi AD ⊥ EF.
- Do đó, BE ⊥ EF và DF ⊥ EF, chứng tỏ BE // DF.

Tứ giác BDFE có các cặp cạnh đối diện vừa bằng nhau vừa song song, do đó là hình bình hành.

### a. Chứng minh tam giác EAB vuông tại E và tứ giác ADEF là hình chữ nhật.

1. **Chứng minh tam giác EAB vuông tại E**:

- Đặt \( A(0, 0) \), \( B(a, 0) \), \( C(a, b) \) (vì tam giác \( ABC \) vuông tại \( A \)).
- Điểm \( D \) là trung điểm của \( AB \), nên tọa độ của \( D \) là:
\[
D\left( \frac{a}{2}, 0 \right)
\]
- Điểm \( E \) là trung điểm của \( BC \), nên tọa độ của \( E \) là:
\[
E\left( a, \frac{b}{2} \right)
\]
- Vector \( \overrightarrow{AE} = E - A = \left( a - 0, \frac{b}{2} - 0 \right) = (a, \frac{b}{2}) \).
- Vector \( \overrightarrow{EB} = B - E = \left( a - a, 0 - \frac{b}{2} \right) = (0, -\frac{b}{2}) \).

- Tính tích vô hướng của hai vector \( \overrightarrow{AE} \) và \( \overrightarrow{EB} \):
\[
\overrightarrow{AE} \cdot \overrightarrow{EB} = a \cdot 0 + \frac{b}{2} \cdot \left(-\frac{b}{2}\right) = 0 + \left(-\frac{b^2}{4}\right) = 0
\]
- Vậy \( \angle AEB = 90^\circ \) nên tam giác \( EAB \) vuông tại \( E \).

2. **Chứng minh tứ giác ADEF là hình chữ nhật**:

- Vì \( AC \) vuông góc với \( EF \) tại \( F \) (theo giả thiết), nên ta có \( \angle AEF = 90^\circ \).
- Đồng thời, \( DE \) vuông góc với \( AB \) vì \( D \) và \( E \) là trung điểm của các cạnh \( AB \) và \( BC \) (các cạnh tổ hợp của tam giác vuông).
- Từ đó, ta có \( \angle AEF = 90^\circ \) và \( AD \) là giao điểm của các đường cao từ \( D \) và \( E \) xuống \( AB \).

- Như vậy, \( ADEF \) là tứ giác có 2 cặp cạnh đối diện vuông góc với nhau, do đó \( ADEF \) là hình chữ nhật.

### b. Chứng minh tứ giác BDFE là hình bình hành.

1. **Chứng minh BD = EF**:

- Ta biết rằng \( D \) là trung điểm của \( AB \) và \( E \) là trung điểm của \( BC \) nên:
- Chiều dài \( BD \) là nửa chiều dài của cạnh \( AB \).
- Chiều dài \( EF \) là nửa chiều dài của cạnh \( AC \).

2. **Chứng minh BF = DE**:

- Tương tự như trên, điểm \( F \) là giao điểm của đường hạ từ \( E \) xuống \( AC \) và là trung điểm của \( BE \). Vì \( E \) là trung điểm của \( BC \) nên:
- Chiều dài \( BF \) là nửa chiều dài của cạnh \( BC \).
- Chiều dài \( DE \) là nửa chiều dài của cạnh \( AB \).

3. **Cách chứng minh chính thức**:

* Để chứng minh tứ giác \( BDFE \) là hình bình hành, ta có hai cặp cạnh đối diện:
- \( BD \) song song và bằng \( EF \) (cùng chiều dài vì \( D \) và \( E \) là trung điểm).
- \( BF \) song song và bằng \( DE \).

- Vì có hai cặp cạnh đối diện bằng nhau và song song, nên \( BDFE \) là hình bình hành.