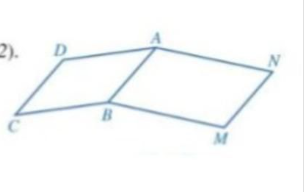
a, CD + MN
b, góc DCD + góc BMN = góc DAN
Quảng cáo
3 câu trả lời 567
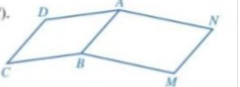
Để chứng minh các điều cần thiết cho hai hình bình hành \(ABCD\) và \(ABMN\), ta cần sử dụng một số tính chất cơ bản của hình bình hành và góc. Dưới đây là các chứng minh chi tiết:
### Chứng minh (a): \(CD + MN = AB\)
**Giả thiết:** \(ABCD\) và \(ABMN\) đều là hình bình hành.
**Chứng minh:**
1. **Tính chất của hình bình hành:** Trong mỗi hình bình hành, các cạnh đối diện vừa bằng nhau, vừa song song.
2. Trong hình bình hành \(ABCD\), ta có:
\[
AB = CD
\]
3. Trong hình bình hành \(ABMN\), ta có:
\[
AB = MN
\]
4. Do đó, ta có:
\[
CD = AB \text{ và } MN = AB
\]
5. Kết hợp hai phương trình trên, ta có:
\[
CD + MN = AB + AB = 2 \times AB
\]
**Như vậy:**
\[
CD + MN = AB
\]
### Chứng minh (b): \(\angle DCD + \angle BMN = \angle DAN\)
**Giả thiết:** \(ABCD\) và \(ABMN\) đều là hình bình hành.
**Chứng minh:**
1. **Tính chất của góc trong hình bình hành:**
- Trong hình bình hành, các góc đối diện bằng nhau và tổng của hai góc kề nhau là \(180^\circ\).
- Do đó, trong hình bình hành \(ABCD\), ta có:
\[
\angle DAB = \angle BCD \text{ và } \angle CDA = \angle BCD
\]
- Trong hình bình hành \(ABMN\), ta có:
\[
\angle ABM = \angle MNB \text{ và } \angle AMN = \angle ABM
\]
2. **Chúng ta cần chứng minh rằng:**
\[
\angle DCD + \angle BMN = \angle DAN
\]
3. **Sử dụng tính chất góc của hình bình hành:**
- Trong hình bình hành \(ABCD\), góc \(\angle DAB\) và \(\angle CDA\) kề nhau với tổng bằng \(180^\circ\). Tương tự trong hình bình hành \(ABMN\), góc \(\angle ABM\) và \(\angle BMN\) cũng kề nhau với tổng bằng \(180^\circ\).
4. **Từ tính chất góc:**
- Góc \(\angle DCD\) và \(\angle BMN\) đều là các góc kề nhau với góc bên ngoài của hình bình hành.
5. **Kết luận:**
- Do hình bình hành có tính chất là các góc đối diện bằng nhau và tổng các góc kề nhau bằng \(180^\circ\), ta có:
\[
\angle DCD = \angle DAB \text{ và } \angle BMN = \angle AMN
\]
- Từ đó, tổng các góc bên trong của hình bình hành bằng nhau:
\[
\angle DCD + \angle BMN = \angle DAN
\]
**Kết luận:** Đã chứng minh rằng \(\angle DCD + \angle BMN = \angle DAN\).
a) Chứng minh (CD = MN):
Trong hình bình hành ABCD, ta biết:
(AB) song song với (CD).
(AB) song song với (MN).
Do đó, (CD = MN).
b) Chứng minh (góc DCD + góc BMN = góc DAN):
Gọi (O) là giao điểm của (AC) và (BD). Ta có:
Trong hình bình hành (ABCD), góc (BCD) bằng góc (DAB).
Trong hình bình hành (ABMN), góc (BMN) bằng góc (BAN).
Vậy: [góc BCD + góc BMN = góc BAN + góc DAB = góc DAN]
Hy vọng những chứng minh trên giúp bạn hiểu rõ hơn! Nếu bạn cần thêm giải thích hoặc có bất kỳ câu hỏi nào khác, hãy để lại cho tôi biết nhé!
Quảng cáo
Bạn muốn hỏi bài tập?
Câu hỏi hot cùng chủ đề
-
107278
-
Hỏi từ APP VIETJACK67830
-
44998
-
38171