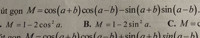Để rút gọn biểu thức \( M = \cos(a+b)\cos(a-b) - \sin(a+b)\sin(a-b) \), ta sử dụng công thức rút gọn cosinus:

\[ \cos A \cos B - \sin A \sin B = \cos(A+B) \]

Áp dụng công thức này vào biểu thức \( M \):

\[ M = \cos(a+b)\cos(a-b) - \sin(a+b)\sin(a-b) \]
\[ M = \cos((a+b) - (a-b)) \]
\[ M = \cos(2b) \]

Vậy, biểu thức đã được rút gọn thành \( M = \cos(2b) \).

Để rút gọn biểu thức \( M = \cos(a+b)\cos(a-b) - \sin(a+b)\sin(a-b) \), ta sẽ sử dụng công thức hạ bậc của hàm lượng giác. Cụ thể, ta sẽ áp dụng công thức tổng và hiệu cho các hàm lượng giác:

### Công thức cần sử dụng

Công thức hạ bậc liên quan đến tổng và hiệu của các hàm lượng giác là:
\[ \cos(x) \cos(y) - \sin(x) \sin(y) = \cos(x + y) \]

Áp dụng công thức này cho biểu thức \( M \), ta có:
\[ \cos(a+b) \cos(a-b) - \sin(a+b) \sin(a-b) = \cos((a+b) + (a-b)) \]

### Tính toán

1. **Tính tổng \( (a+b) + (a-b) \):**
\[
(a+b) + (a-b) = a + b + a - b = 2a
\]

2. **Áp dụng vào công thức:**
\[
\cos((a+b) + (a-b)) = \cos(2a)
\]

### Kết quả

Vậy, biểu thức \( M \) rút gọn được là:
\[ M = \cos(2a) \]

Hy vọng điều này giúp em hiểu rõ hơn về cách rút gọn biểu thức lượng giác!

Từ công thức biến đổi lượng giác, ta có:

\[
\cos(a + b) \cos(a - b) - \sin(a + b) \sin(a - b) = \cos((a+b) + (a-b)) = \cos(a)
\]

### Chi tiết các bước:

1. **Sử dụng công thức đồng nhất** Theo định lý của cosine, ta có thể thay thế:

\[
\cos(A) \cos(B) - \sin(A) \sin(B)