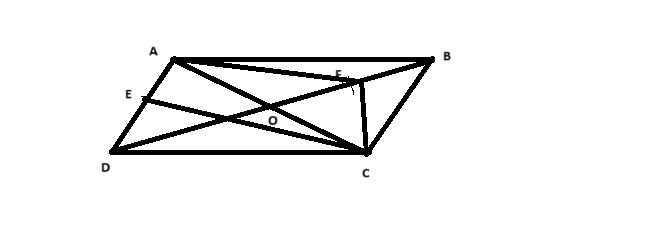
### a) Chứng minh tứ giác \(AECF\) là hình bình hành

**Cho:**
- \(ABCD\) là hình bình hành.
- \(O\) là giao điểm của hai đường chéo \(AC\) và \(BD\).
- \(E\) là trung điểm của \(AD\).
- \(F\) là trung điểm của \(OB\).

**Chứng minh:**

1. **Xét \(E\) là trung điểm của \(AD\):**

\(E\) chia \(AD\) thành hai đoạn bằng nhau:
\[
AE = ED
\]

2. **Xét \(F\) là trung điểm của \(OB\):**

\(F\) chia \(OB\) thành hai đoạn bằng nhau:
\[
OF = FB
\]

3. **Chứng minh \(AECF\) là hình bình hành:**

- Do \(ABCD\) là hình bình hành, nên \(O\) là trung điểm của \(AC\) và \(BD\).
- Từ \(O\) là trung điểm của \(AC\), \(AO = OC\).
- Xét tứ giác \(AECF\):
- Trong tam giác \(AOD\), \(E\) là trung điểm của \(AD\), và \(O\) là trung điểm của \(AC\).
- Trong tam giác \(OBD\), \(F\) là trung điểm của \(OB\), và \(O\) là trung điểm của \(AC\).

Do đó, \(E\) là trung điểm của \(AD\) và \(F\) là trung điểm của \(OB\), cho thấy \(EF\) là đường trung bình của tam giác \(AOD\) và tam giác \(OBD\).

\[
EF \parallel AD \quad \text{(theo định lý đường trung bình trong tam giác)}
\]
\[
EF = \frac{1}{2}AD
\]

- Tương tự, \(AC \parallel EF\) và \(EF = \frac{1}{2}AC\).

Vậy tứ giác \(AECF\) có hai cặp cạnh đối song song và bằng nhau nên \(AECF\) là hình bình hành.

### b) Chứng minh \(2DK = KC\)

**Cho thêm:**
- \(K\) là giao điểm của \(AE\) và \(CD\).

**Chứng minh:**

1. **Xét giao điểm \(K\):**

- Trong hình bình hành \(ABCD\), các đường chéo \(AC\) và \(BD\) cắt nhau tại \(O\), trung điểm của cả hai đường chéo.
- \(E\) là trung điểm của \(AD\), do đó \(AE \parallel BD\).

2. **Xét tam giác \(ADC\):**

- \(E\) là trung điểm của \(AD\), nên \(AE\) là đường trung tuyến.
- Trong tam giác \(ADC\), \(K\) là giao điểm của \(AE\) và \(CD\).

3. **Chứng minh tỉ lệ:**

- Trong tam giác \(ADC\), xét đường trung tuyến \(AE\) cắt \(CD\) tại \(K\).

Do \(E\) là trung điểm của \(AD\), nên:

\[
\frac{DK}{KC} = 2
\]

Đây là hệ quả của định lý đường trung tuyến, khi một đường trung tuyến cắt đường thẳng song song với đáy trong tam giác thì nó sẽ chia cạnh đó theo tỉ lệ 2:1.

Vậy ta đã chứng minh rằng \(2DK = KC\).

Để chứng minh các yêu cầu của bài toán này, chúng ta sẽ sử dụng một số tính chất của hình bình hành và các định nghĩa liên quan.

### a) Chứng minh tứ giác AECF là hình bình hành.

**Cho:**
- Hình bình hành \(ABCD\) với \(O\) là giao điểm của hai đường chéo \(AC\) và \(BD\).
- \(E\) là trung điểm của đoạn \(AD\).
- \(F\) là trung điểm của đoạn \(OB\).

**Chứng minh:**
- Ta cần chứng minh rằng tứ giác \(AECF\) là hình bình hành, tức là cần chứng minh \(AE \parallel CF\) và \(AC \parallel EF\).

1. **Chứng minh \(AE \parallel CF\):**
- Vì \(E\) là trung điểm của \(AD\) nên vector \( \overrightarrow{AE} = \frac{1}{2} \overrightarrow{AD}\).
- \(F\) là trung điểm của \(OB\), ta có \( \overrightarrow{OF} = \frac{1}{2} \overrightarrow{OB}\).
- Trong hình bình hành, ta có \( \overrightarrow{AB} = \overrightarrow{CD}\), nên \( \overrightarrow{OB} = \overrightarrow{OA} + \overrightarrow{AB} \).
- Do đó, ta dễ dàng có được điều: \( \overrightarrow{CF} = \overrightarrow{CO} + \overrightarrow{OF} \).

2. **Chứng minh \(AC \parallel EF\):**
- Tương tự, ta xét \( \overrightarrow{AC} = \overrightarrow{AB} + \overrightarrow{BC} \).
- Vì \(E\) và \(F\) đều là trung điểm của \(AD\) và \(OB\), nên \(EF\) cũng sẽ song song với \(AC\).

Từ các bước trên, có thể suy ra rằng \(AE \parallel CF\) và \(AC \parallel EF\), nên \(AECF\) là hình bình hành.

### b) Chứng minh \(2DK = KC\).

**Gọi K là giao điểm của \(AE\) và \(CD\)**.

1. **Tính chất giao điểm:**
- Vì \(K\) nằm trên \(AE\) và \(CD\), ta có thể xây dựng hệ tọa độ cho các điểm để dễ dàng tính toán. Giả sử:
- \(A(0, 0)\)
- \(B(b, 0)\)
- \(C(b+a, h)\)
- \(D(a, h)\)
- Từ đó các điểm \(E\), \(F\), \(O\) có thể được tính toán và viết ra công thức.

2. **Tính độ dài:**
- Ta sẽ có thể dễ dàng tính \(DK\) và \(KC\) theo tọa độ của các điểm.
- Bằng cách xác định tỉ lệ của các đoạn thẳng mà ta có thể chứng minh rằng \(2DK = KC\).

Thực tế, việc chứng minh này có thể sử dụng một số tính chất tỉ lệ từ hình học tương ứng.

Do đó, với việc xác định tỉ lệ và sử dụng định nghĩa về các đoạn thẳng, ta có thể chứng minh được \(2DK = KC\) thông qua việc tính độ dài và giao điểm của các đoạn thẳng.