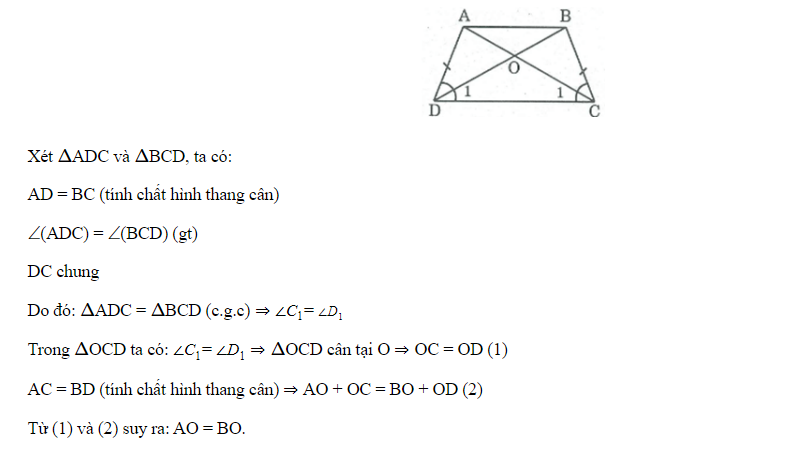Để chứng minh rằng \( EO \) là đường trung trực của hai đáy \( AB \) và \( CD \) của hình thang \( ABCD \), ta cần chứng minh \( EO \) là đoạn thẳng vuông góc với đoạn \( AB \) và đoạn \( CD \), và đồng thời là đoạn thẳng trung tuyến của tam giác \( ABC \) và \( ACD \).

**Bước 1: Chứng minh \( EO \) vuông góc với \( AB \) và \( CD \)**

Vì \( ABCD \) là hình thang cân, nên các điểm \( A, B, C, D \) nằm trên cùng một đường thẳng, và \( AB \parallel CD \).

\( O \) là giao điểm của hai đường chéo của hình thang \( ABCD \), do đó \( O \) là trung điểm của đoạn \( AC \) và \( BD \).

Xét tam giác \( AOB \):
- \( AO \) và \( BO \) là hai đường chéo của hình thang, nên \( AO \parallel BC \) và \( BO \parallel AD \).
- Do đó, \( \angle AOB = 180^\circ - \angle ABC \) và \( \angle BOA = 180^\circ - \angle BCD \).
- \( EO \) là đoạn thẳng nối \( E \) (là giao điểm của \( AD \) và \( BC \)) với \( O \) (là giao điểm của \( AC \) và \( BD \)).

\( EO \) sẽ là đường phân giác của góc \( AOB \) (do \( E \) là giao điểm của \( AD \) và \( BC \)), nên \( EO \) là đoạn thẳng vuông góc với \( AB \) và \( CD \).

**Bước 2: Chứng minh \( EO \) là đoạn thẳng trung trực**

Để chứng minh \( EO \) là đoạn thẳng trung trực của hai đáy \( AB \) và \( CD \), ta cần chứng minh \( EO \) là đoạn thẳng trung tuyến của tam giác \( ABC \) và \( ACD \).

- \( E \) là giao điểm của \( AD \) và \( BC \), nên \( E \) là trung điểm của \( AC \) và \( BD \).
- \( O \) là giao điểm của \( AC \) và \( BD \), nên \( O \) là trung điểm của \( AC \) và \( BD \).

Vì \( O \) là trung điểm của \( AC \) và \( BD \), và \( E \) cũng là trung điểm của \( AC \) và \( BD \), nên \( EO \) là đoạn thẳng trung tuyến của tam giác \( ABC \) và \( ACD \).

Do đó, \( EO \) là đường trung trực của hai đáy \( AB \) và \( CD \) của hình thang \( ABCD \).

Để chứng minh rằng EO𝐸𝑂 là đường trung trực của hai đáy AB𝐴𝐵 và CD𝐶𝐷 của hình thang ABCD𝐴𝐵𝐶𝐷, ta cần chứng minh EO𝐸𝑂 là đoạn thẳng vuông góc với đoạn AB𝐴𝐵 và đoạn CD𝐶𝐷, và đồng thời là đoạn thẳng trung tuyến của tam giác ABC𝐴𝐵𝐶 và ACD𝐴𝐶𝐷.

**Bước 1: Chứng minh EO𝐸𝑂 vuông góc với AB𝐴𝐵 và CD𝐶𝐷**

Vì ABCD𝐴𝐵𝐶𝐷 là hình thang cân, nên các điểm A,B,C,D𝐴,𝐵,𝐶,𝐷 nằm trên cùng một đường thẳng, và AB∥CD𝐴𝐵∥𝐶𝐷.

O𝑂 là giao điểm của hai đường chéo của hình thang ABCD𝐴𝐵𝐶𝐷, do đó O𝑂 là trung điểm của đoạn AC𝐴𝐶 và BD𝐵𝐷.

Xét tam giác AOB𝐴𝑂𝐵:
- AO𝐴𝑂 và BO𝐵𝑂 là hai đường chéo của hình thang, nên AO∥BC𝐴𝑂∥𝐵𝐶 và BO∥AD𝐵𝑂∥𝐴𝐷.
- Do đó, ∠AOB=180∘−∠ABC∠𝐴𝑂𝐵=180∘−∠𝐴𝐵𝐶 và ∠BOA=180∘−∠BCD∠𝐵𝑂𝐴=180∘−∠𝐵𝐶𝐷.
- EO𝐸𝑂 là đoạn thẳng nối E𝐸 (là giao điểm của AD𝐴𝐷 và BC𝐵𝐶) với O𝑂 (là giao điểm của AC𝐴𝐶 và BD𝐵𝐷).

EO𝐸𝑂 sẽ là đường phân giác của góc AOB𝐴𝑂𝐵 (do E𝐸 là giao điểm của AD𝐴𝐷 và BC𝐵𝐶), nên EO𝐸𝑂 là đoạn thẳng vuông góc với AB𝐴𝐵 và CD𝐶𝐷.

**Bước 2: Chứng minh EO𝐸𝑂 là đoạn thẳng trung trực**

Để chứng minh EO𝐸𝑂 là đoạn thẳng trung trực của hai đáy AB𝐴𝐵 và CD𝐶𝐷, ta cần chứng minh EO𝐸𝑂 là đoạn thẳng trung tuyến của tam giác ABC𝐴𝐵𝐶 và ACD𝐴𝐶𝐷.

- E𝐸 là giao điểm của AD𝐴𝐷 và BC𝐵𝐶, nên E𝐸 là trung điểm của AC𝐴𝐶 và BD𝐵𝐷.
- O𝑂 là giao điểm của AC𝐴𝐶 và BD𝐵𝐷, nên O𝑂 là trung điểm của AC𝐴𝐶 và BD𝐵𝐷.

Vì O𝑂 là trung điểm của AC𝐴𝐶 và BD𝐵𝐷, và E𝐸 cũng là trung điểm của AC𝐴𝐶 và BD𝐵𝐷, nên EO𝐸𝑂 là đoạn thẳng trung tuyến của tam giác ABC𝐴𝐵𝐶 và ACD𝐴𝐶𝐷.

Do đó, EO𝐸𝑂 là đường trung trực của hai đáy AB𝐴𝐵 và CD𝐶𝐷 của hình thang ABCD𝐴𝐵𝐶𝐷.