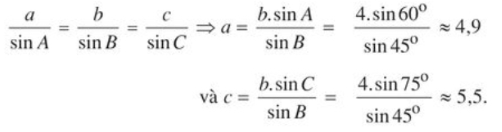Quảng cáo
2 câu trả lời 1207
a)
Ta có:
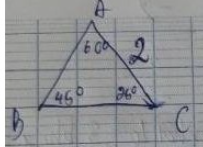
- Trong tam giác ABC, tổng các góc bằng 180°, nên C = 180° - A - B = 180° - 60° - 45° = 75°.
- Sử dụng định lý sin trong tam giác ABC:
a/sinA = b/sinB = c/sinC
=> a/sin60° = 4/sin45° = c/sin75°
=> a = 4sin60°/sin45° ≈ 4.62
=> c = 4sin75°/sin45° ≈ 5.65
Vậy, cạnh a ≈ 4.62 và cạnh c ≈ 5.65.
b)
Ta có:
- Trong tam giác ABC, sử dụng định lý sin:
a/sinA = 2R
=> 6/sin60° = 2R
=> R = 6/(2sin60°) = 6/(2*√3/2) = 6/√3 = 2√3
Vậy, bán kính đường tròn ngoại tiếp tam giác ABC là R = 2√3.
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
 Đã trả lời bởi chuyên gia
89274
Đã trả lời bởi chuyên gia
89274 -
 Đã trả lời bởi chuyên gia
59907
Đã trả lời bởi chuyên gia
59907 -
Hỏi từ APP VIETJACK
 Đã trả lời bởi chuyên gia
59247
Đã trả lời bởi chuyên gia
59247 -
 Đã trả lời bởi chuyên gia
50935
Đã trả lời bởi chuyên gia
50935 -
Hỏi từ APP VIETJACK
 Đã trả lời bởi chuyên gia
48417
Đã trả lời bởi chuyên gia
48417 -
 Đã trả lời bởi chuyên gia
38650
Đã trả lời bởi chuyên gia
38650
Gửi báo cáo thành công!