a.Tính AD
b.Tính diện tính hình thang
Quảng cáo
1 câu trả lời 419
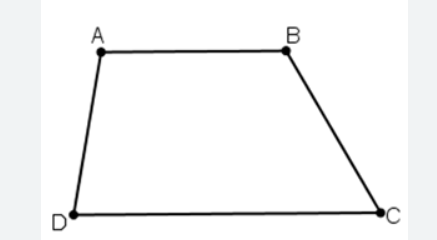
Cho hình thang ABCD có đáy nhỏ AB song song với đáy lớn CD và \(\angle D = 60^\circ\), \(\angle C = 30^\circ\). Biết AB = 2 cm và CD = 6 cm.
### a. Tính AD
Để tính AD, chúng ta có thể sử dụng định lý lượng giác trong tam giác vuông.
1. Đầu tiên, ta xác định chiều cao \(h\) của hình thang từ điểm D và C xuống đường thẳng AB.
2. Vẽ đường cao \( DE \) từ \( D \) đến \( AB \), vuông góc với \( AB \).
3. Vì \( \angle D = 60^\circ \), tam giác \( ADE \) là tam giác vuông với góc \( \angle ADE = 30^\circ \) và \( \angle AED = 60^\circ \).
Sử dụng định lý lượng giác:
\[ DE = AD \cdot \sin 60^\circ \]
\[ DE = AD \cdot \frac{\sqrt{3}}{2} \]
Và trong tam giác \( DCE \):
\[ CE = CD - AB \]
\[ CE = 6 - 2 = 4 \, cm \]
Vì \( \angle C = 30^\circ \):
\[ DE = CE \cdot \tan 30^\circ \]
\[ DE = 4 \cdot \frac{\sqrt{3}}{3} = \frac{4\sqrt{3}}{3} \]
Bây giờ, ta có thể tìm \( AD \):
\[ AD = \frac{DE}{\sin 60^\circ} \]
\[ AD = \frac{\frac{4\sqrt{3}}{3}}{\frac{\sqrt{3}}{2}} = \frac{4\sqrt{3}}{3} \cdot \frac{2}{\sqrt{3}} = \frac{4 \cdot 2}{3} = \frac{8}{3} \, cm \]
### b. Tính diện tích hình thang
Diện tích hình thang được tính bằng công thức:
\[ S = \frac{1}{2} \cdot (AB + CD) \cdot h \]
Chúng ta đã tính được chiều cao \( h \) bằng \( DE \):
\[ h = DE = \frac{4\sqrt{3}}{3} \]
Do đó, diện tích hình thang:
\[ S = \frac{1}{2} \cdot (2 + 6) \cdot \frac{4\sqrt{3}}{3} \]
\[ S = \frac{1}{2} \cdot 8 \cdot \frac{4\sqrt{3}}{3} \]
\[ S = 4 \cdot \frac{4\sqrt{3}}{3} \]
\[ S = \frac{16\sqrt{3}}{3} \, cm^2 \]
Vậy diện tích hình thang là \( \frac{16\sqrt{3}}{3} \, cm^2 \).
Quảng cáo
Bạn muốn hỏi bài tập?
Câu hỏi hot cùng chủ đề
-
103437
-
Hỏi từ APP VIETJACK68807
-
56608
-
47524
-
44249
-
36842
-
35274


