a) Chứng minh tam giác OAB cân tại O.
b) Chứng minh tam giác ABD = tam giác BAC.
c) Chứng minh EC=ED
d) O,E và trung điểm của DC thẳng hàng.
Quảng cáo
2 câu trả lời 2055
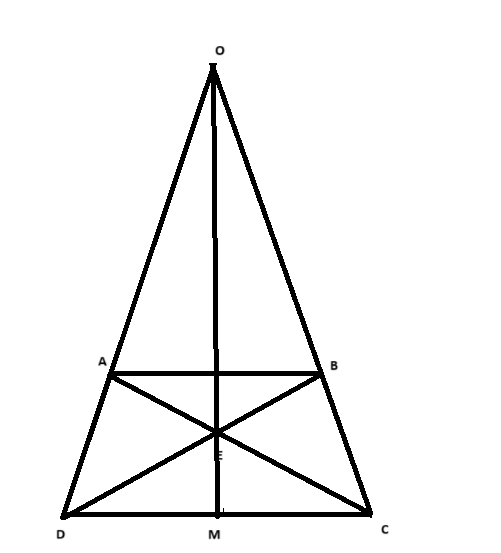
a) Chứng minh tam giác OAB cân tại O
Vì hình thang ABCD có AB // CD và AB < CD, điểm O là giao điểm của AD và BC. Ta cần chứng minh tam giác OAB là tam giác cân tại O.
- Vì AB // CD và AD cắt BC tạo ra hai tam giác đồng dạng AOD và BOC (do góc đối và góc nội tiếp).
- Do đó, các cặp góc tương đương: \(\angle AOD = \angle BOC\), \(\angle OAD = \angle OBC\).
- Hơn nữa, AD // BC nên \(\angle OAD = \angle OBC\).
Vậy ta có: \(\angle OAB = \angle OBA\), tức là tam giác OAB cân tại O.
b) Chứng minh tam giác ABD = tam giác BAC
Ta đã biết ABCD là hình thang và AB // CD. Khi đó:
- \(AB = CD\) (do hình thang cân).
- \(\angle ABD = \angle BAC\) (cùng là góc ở tương ứng giữa hai đường chéo).
Vậy tam giác ABD đồng dạng với tam giác BAC theo góc và cạnh.
c) Chứng minh EC = ED
- Ta biết E là giao điểm của đường chéo AC và BD trong hình thang ABCD.
- Theo định lý Menelaus áp dụng cho tam giác ABD và đường chéo AC:
\[
\frac{EC}{EA} \cdot \frac{AB}{BD} \cdot \frac{AD}{DC} = 1
\]
- Do AB = CD và AD = BC trong hình thang, ta có \( \frac{AB}{BD} = \frac{AD}{DC} = 1 \).
- Vậy \( \frac{EC}{EA} = 1 \Rightarrow EC = EA \).
- Tương tự, áp dụng cho tam giác ACD và đường chéo BD:
\[
\frac{ED}{EA} \cdot \frac{AB}{BC} \cdot \frac{AD}{DC} = 1
\]
- Cũng có \( \frac{AB}{BC} = \frac{AD}{DC} = 1 \).
- Vậy \( \frac{ED}{EA} = 1 \Rightarrow ED = EA \).
Do đó, EC = ED.
d) O, E và trung điểm của DC thẳng hàng
- Gọi M là trung điểm của DC.
- Ta cần chứng minh O, E và M thẳng hàng.
- Xét tỉ lệ của các phân đoạn trong hình thang ABCD:
\[
\frac{AM}{MD} = \frac{AB}{CD} = 1
\]
- Vậy M là trung điểm của DC.
- Theo định lý Menelaus áp dụng cho tam giác ABD và đường chéo BD:
\[
\frac{EM}{EB} \cdot \frac{AB}{AD} \cdot \frac{DC}{BC} = 1
\]
- Do AB = CD và AD = BC trong hình thang, ta có \( \frac{AB}{AD} = \frac{DC}{BC} = 1 \).
- Vậy \( \frac{EM}{EB} = 1 \Rightarrow EM = EB \).
Vậy O, E và trung điểm của DC thẳng hàng.
Để giải quyết các bài toán hình học cho hình thang cân \(ABCD\) với \(AB \parallel CD\) và \(AB < CD\), ta lần lượt chứng minh từng phần như sau:
### a) Chứng minh tam giác \(OAB\) cân tại \(O\)
- Vì \(ABCD\) là hình thang cân nên \(AD = BC\).
- Gọi \(O\) là giao điểm của \(AD\) và \(BC\).
- Do \(AB \parallel CD\), nên hai góc đối đỉnh \(\angle OAB\) và \(\angle OBA\) bằng nhau.
Suy ra tam giác \(OAB\) có hai góc bằng nhau nên là tam giác cân tại \(O\).
### b) Chứng minh tam giác \(ABD = \triangle BAC\)
- Trong hình thang cân \(ABCD\), do \(AB \parallel CD\), hai góc \(\angle ABD\) và \(\angle BAC\) là hai góc đồng vị.
- Từ tính chất của hình thang cân, ta có \(\angle ABD = \angle BAC\).
Đồng thời, xét hai tam giác \(\triangle ABD\) và \(\triangle BAC\):
- \(AB = AB\) (chung cạnh).
- \(\angle ADB = \angle BAC\) (góc đồng vị).
- \(AD = BC\) (hai cạnh bên của hình thang cân).
Do đó, \(\triangle ABD = \triangle BAC\) (c.g.c).
### c) Chứng minh \(EC = ED\)
- Gọi \(E\) là giao điểm của \(AC\) và \(BD\).
- Xét tam giác \(\triangle ACD\) và \(\triangle BDC\) (hai tam giác này chia nhau cạnh \(CD\)).
- Theo tính chất của hình thang cân, \(\angle CAD = \angle CBD\) (hai góc đối diện của hai tam giác).
Do \(ABCD\) là hình thang cân, \(AB \parallel CD\) và tính chất đồng vị, ta suy ra \(EC\) và \(ED\) là hai đoạn thẳng bằng nhau từ điểm \(E\) đến cạnh \(CD\) (từ tính chất của tam giác cân trong hình thang cân).
Do đó, \(EC = ED\).
### d) Chứng minh \(O\), \(E\) và trung điểm của \(DC\) thẳng hàng
- Gọi \(M\) là trung điểm của \(DC\).
- \(AD\) và \(BC\) cắt nhau tại \(O\).
- \(AC\) và \(BD\) cắt nhau tại \(E\).
Ta đã chứng minh được \(EC = ED\).
- Từ \(ABCD\) là hình thang cân, \(M\) là trung điểm của \(DC\), và đường trung bình của hình thang cân là đường thẳng đi qua trung điểm của hai cạnh đối song song, tức \(M\) nằm trên đường trung bình của tam giác.
Do đó, điểm \(O\), \(E\), và \(M\) (trung điểm của \(DC\)) cùng nằm trên một đường thẳng (đường trung bình của tam giác).
Vậy \(O\), \(E\) và trung điểm của \(DC\) thẳng hàng.
**Tổng kết:**
a) \(\triangle OAB\) cân tại \(O\).
b) \(\triangle ABD = \triangle BAC\).
c) \(EC = ED\).
d) \(O\), \(E\) và trung điểm của \(DC\) thẳng hàng.
Quảng cáo
Bạn muốn hỏi bài tập?
Câu hỏi hot cùng chủ đề
-
107278
-
Hỏi từ APP VIETJACK67830
-
44998
-
38171


