Quảng cáo
1 câu trả lời 513
1 năm trước
Ta có:
⦁ x – 1 ≠ 0 khi x ≠ 1.
⦁ 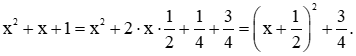
Với mọi x ta luôn có 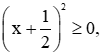 nên
nên 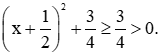
⦁ x3 – 1 = (x – 1)(x2 + x + 1).
Khi đó x3 – 1 ≠ 0 khi (x – 1)(x2 + x + 1) ≠ 0, hay x – 1 ≠ 0, tức là x ≠ 1.
Vì vậy, điều kiện xác định của phương trình đã cho là x ≠ 1.
Quy đồng mẫu của phương trình, ta được:
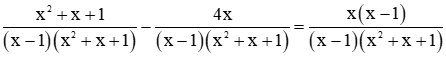
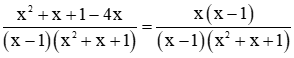
Khử mẫu của phương trình, ta được: x2 + x + 1 – 4x = x(x – 1). (*)
Giải phương trình (*):
x2 + x + 1 – 4x = x(x – 1)
x2 – 3x + 1 = x2 – x
x2 – 3x + 1 – x2 + x = 0
–2x = –1
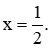
Giá trị 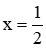 thỏa mãn điều kiện xác định của phương trình.
thỏa mãn điều kiện xác định của phương trình.
Vậy phương trình đã cho có nghiệm là 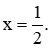
Quảng cáo
Bạn muốn hỏi bài tập?
Câu hỏi hot cùng chủ đề
-
103349
-
Hỏi từ APP VIETJACK68744
-
56565
-
47490
-
44183
-
36818
-
35211
Gửi báo cáo thành công!