a) Chứng minh tứ giác BCFK nội tiếp được đường tròn
Quảng cáo
2 câu trả lời 310
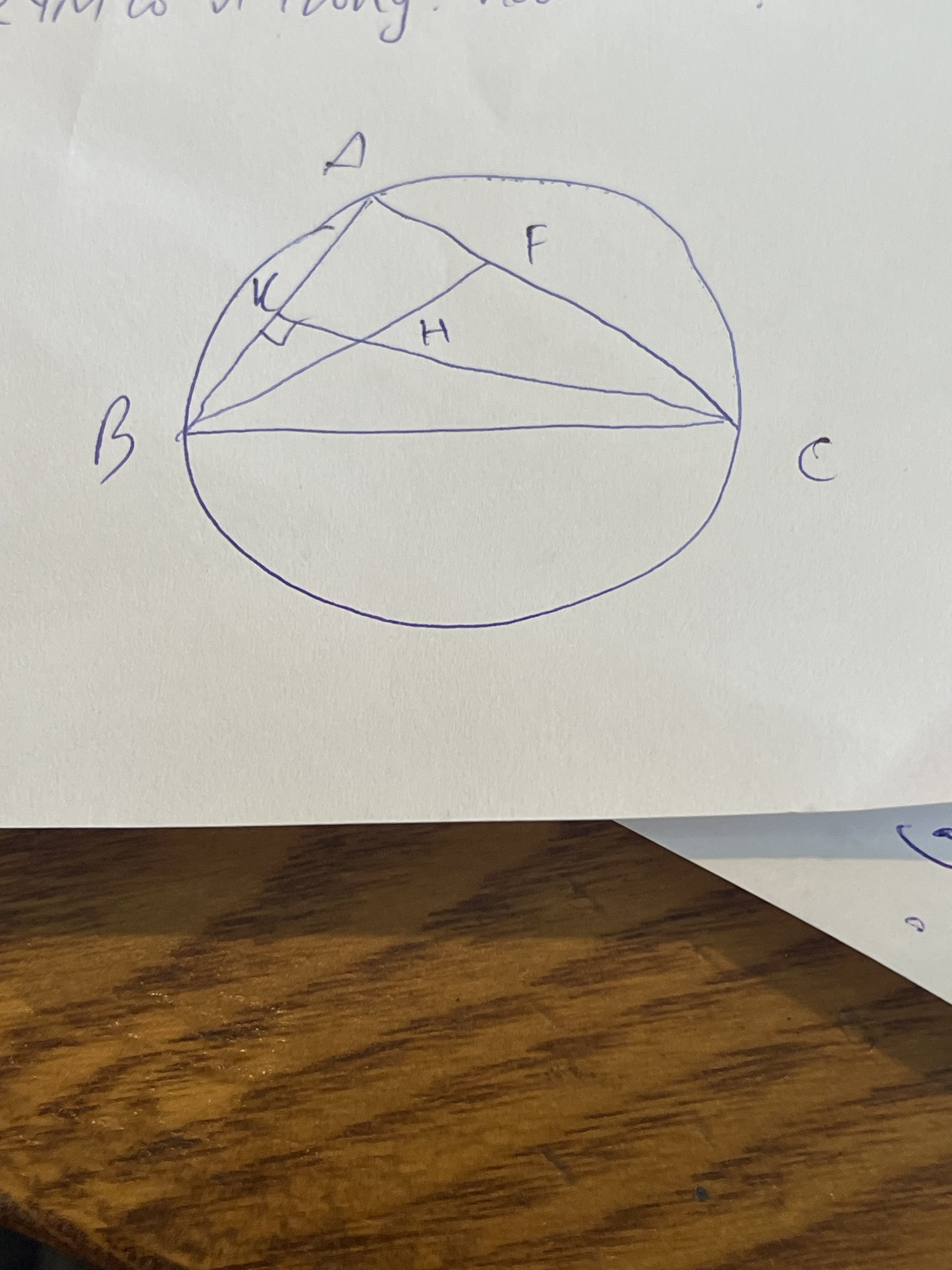 Xét tg BCFK:
Xét tg BCFK:
^ BKC=90•(CK là đường cao)
^BFC=90•(BF là đường cao)
=> K, F thuộc đường tròn đường kính BC(qtdt)
=> TG BCFK nt đường tròn đường kính BC
Để chứng minh tứ giác \( BCFK \) nội tiếp vào đường tròn, ta cần chứng minh rằng góc \( \angle BFK \) và \( \angle BCK \) cùng nằm trên cùng một dây cung của đường tròn.
Vì tam giác \( ABC \) nội tiếp đường tròn \( O \), nên góc \( \angle BAC \) và \( \angle BOC \) là góc hai nửa trên cùng một dây cung.
Do đó, ta có:
\[ \angle BFK = \angle BAC \]
\[ \angle BCK = \angle BOC \]
Vì \( \angle BAC = \angle BOC \) (cùng nằm trên cùng một dây cung), nên:
\[ \angle BFK = \angle BCK \]
Vậy tứ giác \( BCFK \) nội tiếp vào đường tròn.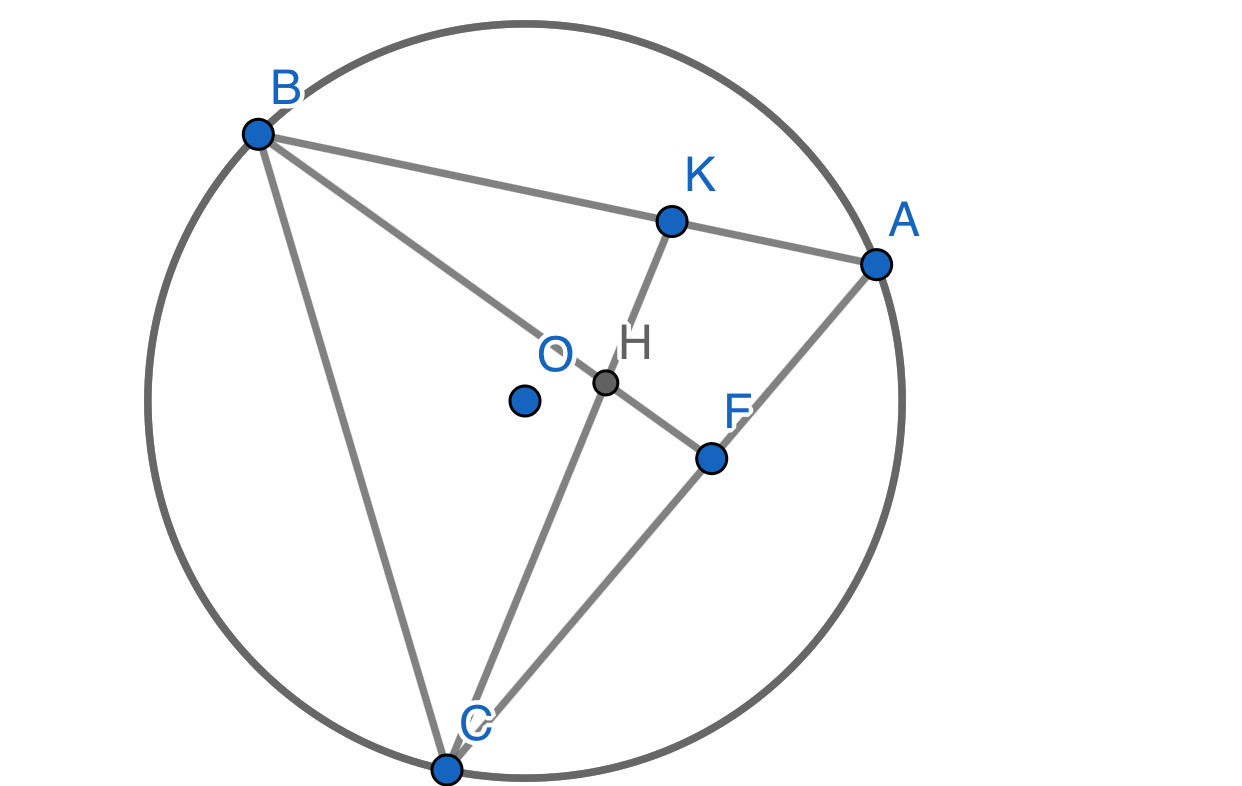
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
 Đã trả lời bởi chuyên gia
103520
Đã trả lời bởi chuyên gia
103520 -
Hỏi từ APP VIETJACK
 Đã trả lời bởi chuyên gia
68861
Đã trả lời bởi chuyên gia
68861 -
 Đã trả lời bởi chuyên gia
56682
Đã trả lời bởi chuyên gia
56682 -
 Đã trả lời bởi chuyên gia
47564
Đã trả lời bởi chuyên gia
47564 -
 Đã trả lời bởi chuyên gia
44351
Đã trả lời bởi chuyên gia
44351 -
 Đã trả lời bởi chuyên gia
36876
Đã trả lời bởi chuyên gia
36876 -
 Đã trả lời bởi chuyên gia
35387
Đã trả lời bởi chuyên gia
35387


