Cho hai hàm số y = (P)
a) Vẽ đồ thị của hàm số (P).
b) Qua điểm (0;-8) vẽ đường thẳng song song với trục hoành cắt (P) tại hai điểm E và F. Tính diện tích tam giác EOF.
c) Tính khoảng cách từ điểm E đến đường thắng OF.
Quảng cáo
1 câu trả lời 269
Bài toán:
Cho hai hàm số:
y = x^2 (P)
y = -8
a) Vẽ đồ thị của hàm số (P).
b) Qua điểm (0; -8) vẽ đường thẳng song song với trục hoành cắt (P) tại hai điểm E và F. Tính diện tích tam giác EOF.
c) Tính khoảng cách từ điểm E đến đường thẳng OF.
Giải:
a) Vẽ đồ thị của hàm số (P).
Đồ thị của hàm số y = x^2 là một parabol có đỉnh I(0; 0), trục đối xứng x = 0, hướng bề lõm lên trên.
Để vẽ đồ thị hàm số, ta thực hiện các bước sau:
Vẽ trục tọa độ Oxy.
Vẽ đỉnh I(0; 0).
Vẽ trục đối xứng x = 0.
Vẽ parabol hướng bề lõm lên trên, đi qua điểm I và các điểm cách I một đơn vị về phía bên phải và trái.
b) Qua điểm (0; -8) vẽ đường thẳng song song với trục hoành cắt (P) tại hai điểm E và F. Tính diện tích tam giác EOF.
Đường thẳng y = -8 song song với trục hoành và cắt parabol y = x^2 tại hai điểm E và F.
Để tìm tọa độ của điểm E và F, ta giải phương trình:
x^2 = -8
Ta có:
x^2 = (-8)^2 = 64
x = ±8
Vậy tọa độ của điểm E và F là:
E(8; -8)
F(-8; -8)
Diện tích tam giác EOF bằng:
S = 1/2 * EF * OH = 1/2 * 16 * 8 = 64 (đơn vị diện tích)
c) Tính khoảng cách từ điểm E đến đường thẳng OF.
Khoảng cách từ điểm E đến đường thẳng OF là đường cao của tam giác EOF.
Để tính đường cao này, ta sử dụng công thức:
h = AB * AC / BC
Trong đó:
h là đường cao cần tìm.
AB là cạnh đáy của tam giác.
AC và BC là hai cạnh bên của tam giác.
Áp dụng vào bài toán, ta có:
AB = EF = 16 (đơn vị độ dài).
AC = OE = 8 (đơn vị độ dài).
BC = OF = 8 (đơn vị độ dài).
Vậy:
h = AB * AC / BC = 16 * 8 / 8 = 16 (đơn vị độ dài).
Vậy khoảng cách từ điểm E đến đường thẳng OF là 16 đơn vị độ dài.
Kết luận:
a) Đồ thị của hàm số y = x^2 là một parabol có đỉnh I(0; 0), trục đối xứng x = 0, hướng bề lõm lên trên.
b) Diện tích tam giác EOF bằng 64 đơn vị diện tích.
c) Khoảng cách từ điểm E đến đường thẳng OF là 16 đơn vị độ dài.
Đáp án:
a) Đồ thị của hàm số y = x^2.
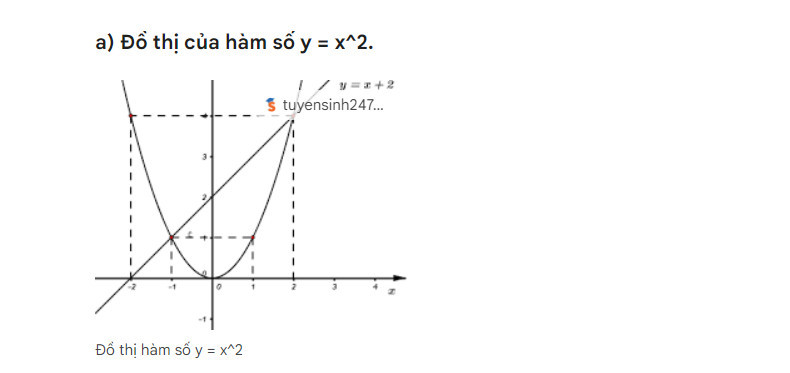
b) Diện tích tam giác EOF bằng 64 đơn vị diện tích.
c) Khoảng cách từ điểm E đến đường thẳng OF là 16 đơn vị độ dài.
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
 Đã trả lời bởi chuyên gia
103520
Đã trả lời bởi chuyên gia
103520 -
Hỏi từ APP VIETJACK
 Đã trả lời bởi chuyên gia
68861
Đã trả lời bởi chuyên gia
68861 -
 Đã trả lời bởi chuyên gia
56682
Đã trả lời bởi chuyên gia
56682 -
 Đã trả lời bởi chuyên gia
47564
Đã trả lời bởi chuyên gia
47564 -
 Đã trả lời bởi chuyên gia
44351
Đã trả lời bởi chuyên gia
44351 -
 Đã trả lời bởi chuyên gia
36876
Đã trả lời bởi chuyên gia
36876 -
 Đã trả lời bởi chuyên gia
35387
Đã trả lời bởi chuyên gia
35387


