Bài 7. Cho tam giác ABC có AB = AC. Gọi M là trung điểm của cạnh BC.
a) Chứng minh tam giác ABM = tam giác ACM và góc AMB = 90 độ .
b) Chứng minh AM là tia phân giác của góc BAC.
c) Trên tia đối của tia MA lấy điểm D sao cho MD = MA. Chứng minh BD // AC.
Quảng cáo
1 câu trả lời 187
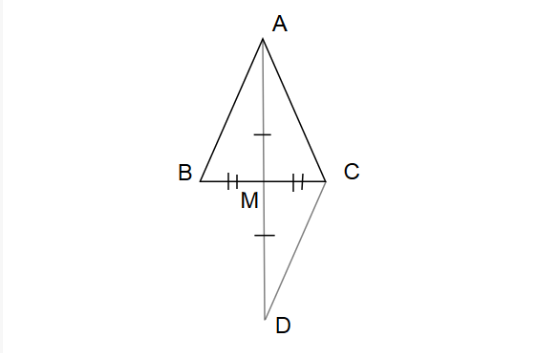
a)
Xét ΔABM và ΔACM ta có:
AB = AC (theo giả thiết);
AM chung
MB = MC (do M là trung điểm của BC)
=> ΔABM = ΔACM (c.c.c).
^BMA=^CMA (hai góc tương ứng).Mà ^BMA+^CMA=180°^BMA=^CMA=90° .
b)
Từ ΔABM = ΔACM
=>^BAM=^CAM
suy ra AM là tia phân giác của góc A.
c)
Xét △ABM và △DCM có :
AM=DM (gt)
^ABM =^DCM ( vì hai góc đối đỉnh )
BM=CM( vì M là trung điểm của BC)
=>△ABM=△DCM(c−g−c)
=> MA = MD
Quảng cáo
Câu hỏi hot cùng chủ đề
-
Hỏi từ APP VIETJACK113530
-
78716
-
56394













