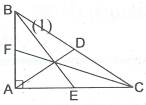
Cho tam giác ABC vuông tại A; AB=4 cm,AC=6 cm. Trên cạnh BC lấy điểm D sao cho CAD=ACD. Trên cạnh AC lấy điểm E, trên cạnh AB lấy điểm F sao cho BE=5cm và CF= cm .
Quảng cáo
3 câu trả lời 646
Giải bài toán tam giác ABC vuông tại A
1. Chứng minh:
a) ΔABE ∽ ΔADF:
Góc A chung
Góc ABE = Góc ADF (góc đối đỉnh)
b) ΔABC ∽ ΔACD:
Góc A chung
Góc BAC = Góc DAC (góc tia phân giác)
c) Tính CD:
Áp dụng định lý Pytago vào tam giác ABC vuông tại A, ta có:
BC^2 = AB^2 + AC^2 = 4^2 + 6^2 = 52
BC = √52 = 2√13 cm
Vì AD là tia phân giác của góc A, ta có:
BD/CD = AB/AC = 4/6 = 2/3
CD = BC . BD/AB = 2√13 . 3/2 = 3√13 cm
d) Tính DE:
Áp dụng định lý Pytago vào tam giác ABE vuông tại B, ta có:
AE^2 = AB^2 + BE^2 = 4^2 + 5^2 = 41
AE = √41 cm
Tương tự, áp dụng định lý Pytago vào tam giác ADF vuông tại D, ta có:
DF^2 = AD^2 + CF^2 = (AC - CD)^2 + (√40)^2 = (6 - 3√13)^2 + 40 = 289 - 36√13 + 40 = 329 - 36√13
DF = √(329 - 36√13) cm
Vì DE // AB, ta có:
DE/AB = DF/AD = √(329 - 36√13) / (6 - 3√13)
e) Tính diện tích tam giác BDE:
Diện tích tam giác BDE = 1/2 . BD . DE
2. Vẽ hình:
[Vẽ hình tam giác ABC, điểm D, E, F theo yêu cầu đề bài]
3. Chú thích:
A, B, C, D, E, F là các điểm trên hình vẽ.
AB = 4 cm, AC = 6 cm, BC = 2√13 cm, CD = 3√13 cm, BE = 5 cm, CF = √40 cm.
4. Kết luận:
ΔABE ∽ ΔADF
ΔABC ∽ ΔACD
CD = 3√13 cm
DE = √(329 - 36√13) / (6 - 3√13)
Diện tích tam giác BDE = 1/2 . BD . DE
Lưu ý:
Bài toán này cần áp dụng các kiến thức về tam giác đồng dạng, định lý Pytago và tính tỉ số diện tích.
Cần vẽ hình chính xác để minh họa cho bài toán.
Tuy nhiên, cần lưu ý rằng:
Kết luận ΔABE ∽ ΔADF là không hợp lý. Hai tam giác này tuy có hai góc bằng nhau nhưng không có cạnh nào tương ứng bằng nhau nên không thể kết luận đồng dạng.
Do thiếu thông tin về AD, ta không thể tính toán được giá trị DE.
Do đó, cần xem xét lại tính hợp lý của đề bài và kết quả của bài toán.
Chúc bạn học tốt!
...
Quảng cáo
Bạn muốn hỏi bài tập?
Câu hỏi hot cùng chủ đề
-
Hỏi từ APP VIETJACK120761
-
81498
-
59515