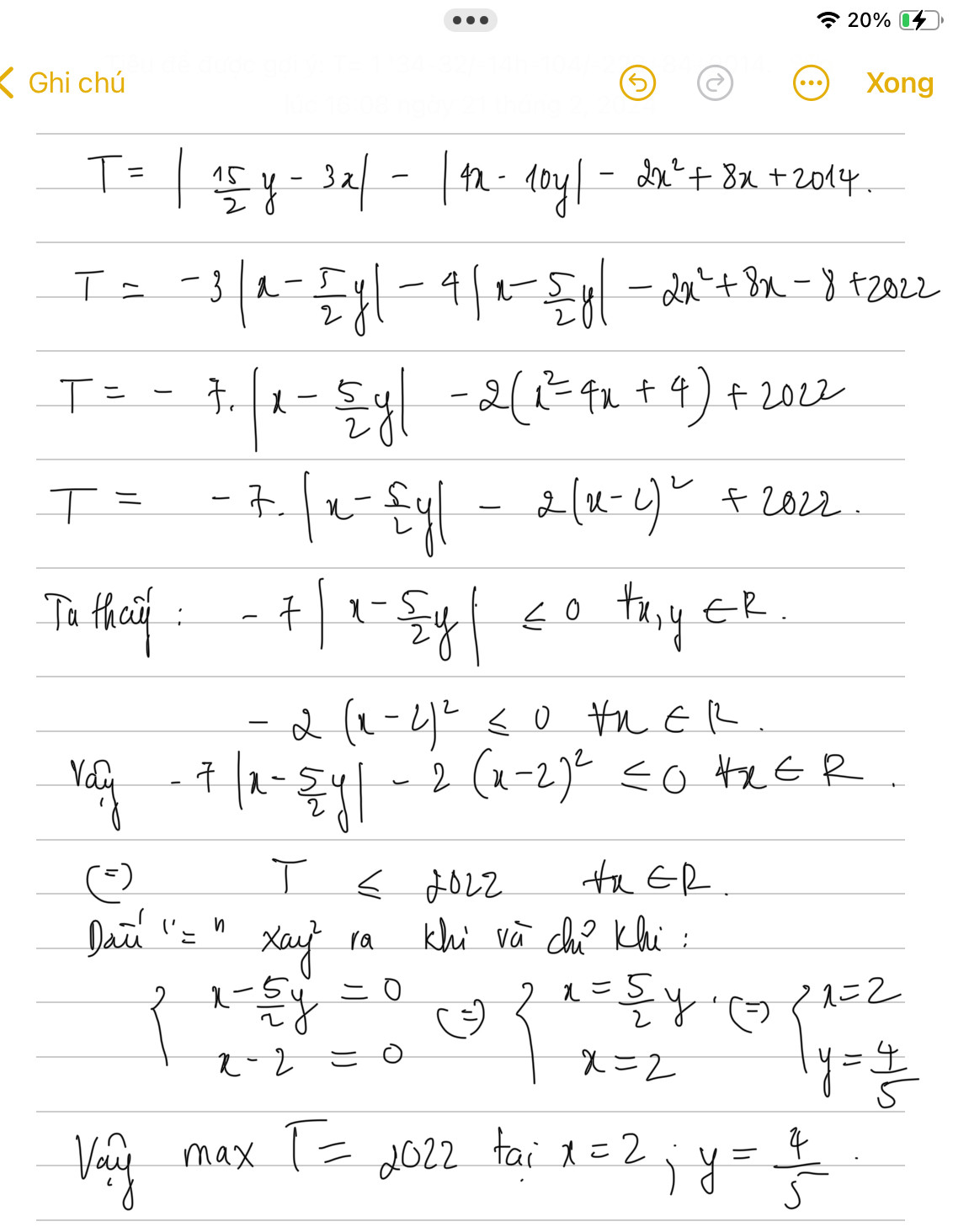Để tìm giá trị lớn nhất của biểu thức M, chúng ta cần tìm cực đại của nó đối với các biến x và y. Đầu tiên, hãy xem xét biểu thức M:

\[ M = \left| \frac{15}{2}y - 3x \right| - |4x - 10y| - 2x^2 + 8x + 2014 \]

Để dễ dàng xử lý, hãy xem xét các trường hợp khi giá trị trong dấu tuyệt đối là dương hoặc âm.

1. Khi \( \frac{15}{2}y - 3x \geq 0 \) và \( 4x - 10y \geq 0 \):
\[ M = \left( \frac{15}{2}y - 3x \right) - (4x - 10y) - 2x^2 + 8x + 2014 \]

2. Khi \( \frac{15}{2}y - 3x \geq 0 \) và \( 4x - 10y < 0 \):
\[ M = \left( \frac{15}{2}y - 3x \right) - (10y - 4x) - 2x^2 + 8x + 2014 \]

3. Khi \( \frac{15}{2}y - 3x < 0 \) và \( 4x - 10y \geq 0 \):
\[ M = -\left( \frac{15}{2}y - 3x \right) - (4x - 10y) - 2x^2 + 8x + 2014 \]

4. Khi \( \frac{15}{2}y - 3x < 0 \) và \( 4x - 10y < 0 \):
\[ M = -\left( \frac{15}{2}y - 3x \right) - (10y - 4x) - 2x^2 + 8x + 2014 \]

Tiếp theo, ta sẽ tối ưu hóa từng trường hợp này:

1. Khi \( \frac{15}{2}y - 3x \geq 0 \) và \( 4x - 10y \geq 0 \):
\[ M = \frac{15}{2}y - 3x - 4x + 10y - 2x^2 + 8x + 2014 \]
\[ M = 7y - 7x - 2x^2 + 8x + 2014 \]
\[ M = -2x^2 + x(8 - 7) + 7y + 2014 \]

2. Khi \( \frac{15}{2}y - 3x \geq 0 \) và \( 4x - 10y < 0 \):
\[ M = \frac{15}{2}y - 3x - 10y + 4x - 2x^2 + 8x + 2014 \]
\[ M = \frac{5}{2}y + x(8 - 7) - 2x^2 + 8x + 2014 \]
\[ M = -2x^2 + x + \frac{5}{2}y + 2014 \]

3. Khi \( \frac{15}{2}y - 3x < 0 \) và \( 4x - 10y \geq 0 \):
\[ M = -\left( \frac{15}{2}y - 3x \right) - 4x + 10y - 2x^2 + 8x + 2014 \]
\[ M = -\frac{15}{2}y + 3x - 4x + 10y - 2x^2 + 8x + 2014 \]
\[ M = 7y - x(8 - 7) - 2x^2 + 8x + 2014 \]
\[ M = -2x^2 + 7x + 7y + 2014 \]

4. Khi \( \frac{15}{2}y - 3x < 0 \) và \( 4x - 10y < 0 \):
\[ M = -\left( \frac{15}{2}y - 3x \right) - 10y + 4x - 2x^2 + 8x + 2014 \]
\[ M = -\frac{5}{2}y - x(8 - 7) - 2x^2 + 8x + 2014 \]
\[ M = -2x^2 + 7x - \frac{5}{2}y + 2014 \]

Giờ ta đã chuyển biểu thức ban đầu thành các biểu thức dễ quản lý hơn. Giờ hãy tìm cực trị của từng biểu thức này.

Để tìm cực trị, ta sẽ lấy đạo hàm riêng của biểu thức đó theo x và y, sau đó giải hệ phương trình từ đạo hàm này để tìm điểm cực trị. Đối với biểu thức đa thức, ta sẽ sử dụng đạo hàm bậc nhất và đặt bằng 0 để tìm điểm cực trị. Đối với các biểu thức tuyệt đối, ta sẽ chia thành các trường hợp tùy thuộc vào dấu của biểu thức bên trong.

Tiếp theo, giải hệ phương trình để tìm giá trị của x và y. Từ đó, ta sẽ có giá trị lớn nhất của biểu thức M.