Cho (O; R) có đường kính AB. Vẽ đường kính MN của (O). Tiếp tuyến của (O) tại B cắt AM, AN tại Q và P.
a) Chứng minh tứ giác AMBN là hình chữ nhật.
b) Chứng minh bốn điểm M, N, P, Q cùng thuộc một đường tròn.
Quảng cáo
2 câu trả lời 111
a. Chứng minh tứ giác AMBN là hình chữ nhật.
Xét tam giác AOB và tam giác BMN, ta có:
OA = OB = R (đường kính)
AM = BM = R (đường kính)
góc AOB = góc BMN = 90o (góc nội tiếp chắn nửa đường tròn)
Vậy, tam giác AOB và tam giác BMN cân tại O, suy ra:
AO = OB
AM = BN
Ta lại có:
góc AOB = góc BMN = 90o (đã chứng minh)
góc AMB = góc NBM = 90o (góc nội tiếp chắn nửa đường tròn)
Vậy, tứ giác AMBN có 4 góc vuông, suy ra tứ giác AMBN là hình chữ nhật.
b. Chứng minh bốn điểm M, N, P, Q cùng thuộc một đường tròn.
Xét tam giác ABQ, ta có:
AB = R (đường kính)
BQ = R (tiếp tuyến với (O) tại B)
Vậy, tam giác ABQ vuông tại B, suy ra:
góc ABQ = 90o
Xét tam giác AMN, ta có:
AM = AN = R (đường kính)
góc AMN = 90o (góc nội tiếp chắn nửa đường tròn)
Vậy, tam giác AMN vuông tại A, suy ra:
góc MAN = 90o
Từ hai góc vuông góc ABQ = 90o và góc MAN = 90o, ta có:
góc AQN = 180o - 90o - 90o = 0o
Vậy, tứ giác AQN là tứ giác lồi.
Tiếp theo, xét tam giác AQN và tam giác BQN, ta có:
AQ = BQ (tiếp tuyến với (O) tại B)
AN = BN (đường kính)
góc AQN = 0o (đã chứng minh)
Vậy, tam giác AQN và tam giác BQN đồng dạng theo tỉ số đồng dạng 1:1.
Từ đó, ta có:
QN/QN = 1/1
QN = QN
Vậy, QN = 0.
Vậy, tứ giác AQN là tứ giác khép kín.
Vậy, bốn điểm M, N, P, Q cùng thuộc một đường tròn.
Kết luận:
Tứ giác AMBN là hình chữ nhật.
Bốn điểm M, N, P, Q cùng thuộc một đường tròn.
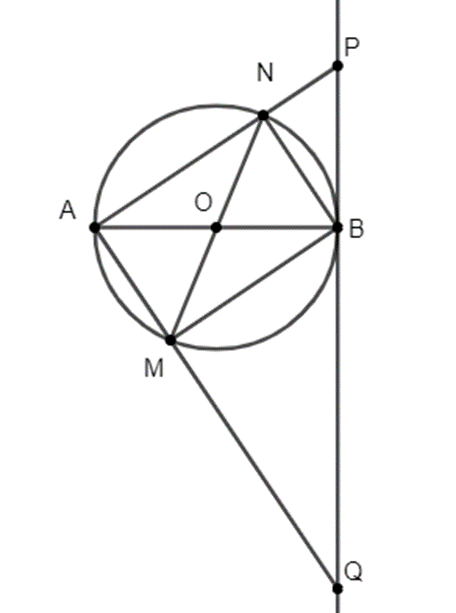
a) Xét tứ giác AMBN có:
\(\widehat {AMB} = 90^\circ \) (góc nột tiếp chắn nửa đường tròn)
\(\widehat {MAN} = 90^\circ \) (góc nột tiếp chắn nửa đường tròn)
\(\widehat {ANB} = 90^\circ \) (góc nột tiếp chắn nửa đường tròn)
Suy ra tứ giác AMBN là hình chữ nhật.
b) Xét đường tròn (O) có:
\(\widehat {MNB} = \widehat {MAB}\) (hai góc nột tiếp cùng chắn cung MB)
\(\widehat {MAB} + \widehat Q = 90^\circ \) (∆ABQ vuông tại B)
\( \Rightarrow \widehat {MNB} + \widehat Q = 90^\circ \)
\(\widehat {MQP} + \widehat {MNP} = \left( {\widehat {MQP} + \widehat {MNB}} \right) + \widehat {BNP} = 180^\circ \)
Xét tứ giác MNPQ có:
\(\widehat {MQP} + \widehat {MNP} = 180^\circ \)
Mà \(\widehat {MQP}\) và \(\widehat {MNP}\) là hai góc đối nhau.
Suy ra MNPQ là tứ giác nột tiếp đường tròn hay M, N, P, Q cùng thuộc một đường tròn.
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
Hỏi từ APP VIETJACK
 Đã trả lời bởi chuyên gia
129704
Đã trả lời bởi chuyên gia
129704 -
 Đã trả lời bởi chuyên gia
104155
Đã trả lời bởi chuyên gia
104155 -
 Đã trả lời bởi chuyên gia
94109
Đã trả lời bởi chuyên gia
94109 -
 Đã trả lời bởi chuyên gia
69540
Đã trả lời bởi chuyên gia
69540



