Cho đường tròn tâm O đường kính AB, vẽ dây CD vuông góc với AB tại H (H nằm giữa O và B). Trên tia CD lấy điểm E nằm ngoài đường tròn, EB cắt đường tròn tại F (F khác B), AF cắt CD tại K.
a) Chứng minh tứ giác BFKH nội tiếp.
b) Chứng minh AB.BH = EB.BF
c) Cho biết AB = 6 cm, AF = 5 cm. Tính diện tích hình quạt tròn BOF ứng với cung nhỏ BF của đường tròn (O) (kết quả làm tròn đến chữ số thập phân thứ nhất).
Quảng cáo
1 câu trả lời 196
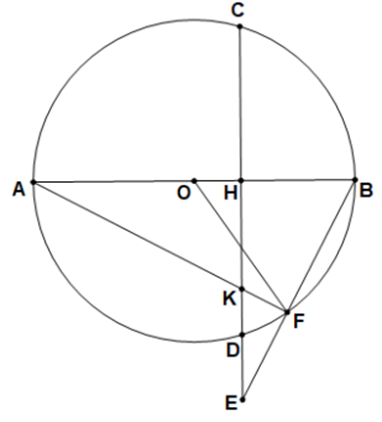
a) Ta có = 90° (AB vuông góc với CD tại H)
= 90° (góc nội tiếp chắn nửa đường tròn)
Suy ra = 180°
Do đó tứ giác BFKH nội tiếp.
b) Xét ∆ABF và ∆EBH có:
= = 90° (cmt)
chung
Do đó ∆ABF ∆EBH (g.g)
Suy ra (các góc tương ứng).
Do đó AB.BH = EB.BF (đpcm)
c) Xét ∆AFB vuông tại F, có: cos = Þ ≈ 33°33’
Suy ra số đo cung nhỏ BF ≈ 67°7’
Diện tích hình quạt là:
S = = ≈ 5,3 (cm2).
Vậy diện tích hình quạt tròn BOF ứng với cung nhỏ BF của đường tròn (O) (kết quả làm tròn đến chữ số thập phân thứ nhất) là 5,3 cm2.
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
 Đã trả lời bởi chuyên gia
103643
Đã trả lời bởi chuyên gia
103643 -
Hỏi từ APP VIETJACK
 Đã trả lời bởi chuyên gia
68927
Đã trả lời bởi chuyên gia
68927 -
 Đã trả lời bởi chuyên gia
56777
Đã trả lời bởi chuyên gia
56777 -
 Đã trả lời bởi chuyên gia
47628
Đã trả lời bởi chuyên gia
47628 -
 Đã trả lời bởi chuyên gia
44434
Đã trả lời bởi chuyên gia
44434 -
 Đã trả lời bởi chuyên gia
36922
Đã trả lời bởi chuyên gia
36922 -
 Đã trả lời bởi chuyên gia
35490
Đã trả lời bởi chuyên gia
35490


