Cho phương trình x4 + mx2 - m - 1 = 0(m là tham số)
a) Giải phương trình khi m = 2
b) Tìm giá trị của m để phương trình có 4 nghiệm phân biệt.
Quảng cáo
2 câu trả lời 1101
b) Đặt x 2 = t (t ≥ 0). Khi đó ta có phương trình: t 2 – mt – m – 1 = 0 (*)
Δ = m 2 - 4(-m - 1) = m 2 + 4m + 4 = m + 2 2
Phương trình đã cho có 4 nghiệm phân biệt khi và chỉ khi phương trình (*) có 2 nghiệm dương phân biệt
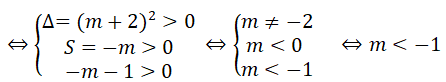
Thay m= 2 vào phương trình ta có :
x4 + 2x2 -2-1=0
=> x4+ 2x2-3=0
Đặt t=x2 điều kiện x>0
Ta có :t2 + 2t - 3=0
Theo hệ thức vi- ét a+b+c=0 --> Pt có 2 nghiệm phân biệt là
t1 = 1 ( TM ); t1 = -3 ( KTM)
+ Với t=1 => x2 =1 = +-1
Vậy pt có 2 nghiệm là x1= 1 ; x2=-1
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
 Đã trả lời bởi chuyên gia
103520
Đã trả lời bởi chuyên gia
103520 -
Hỏi từ APP VIETJACK
 Đã trả lời bởi chuyên gia
68861
Đã trả lời bởi chuyên gia
68861 -
 Đã trả lời bởi chuyên gia
56682
Đã trả lời bởi chuyên gia
56682 -
 Đã trả lời bởi chuyên gia
47564
Đã trả lời bởi chuyên gia
47564 -
 Đã trả lời bởi chuyên gia
44351
Đã trả lời bởi chuyên gia
44351 -
 Đã trả lời bởi chuyên gia
36876
Đã trả lời bởi chuyên gia
36876 -
 Đã trả lời bởi chuyên gia
35387
Đã trả lời bởi chuyên gia
35387


