Trong mặt phẳng Oxy cho ba điểm A(2; 2); B(1; 3); C(– 1; 1
Lời giải Bài 1 trang 78 SBT Toán 10 sách Chân trời sáng tạo hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 10.
Bài 1 trang 78 SBT Toán 10 Tập 2: Trong mặt phẳng Oxy cho ba điểm A(2; 2); B(1; 3); C(– 1; 1).
a) Chứng minh OABC là một hình chữ nhật;
b) Tìm toạ độ tâm I của hình chữ nhật OABC.
Lời giải:
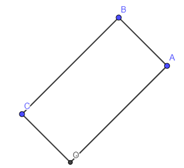
a) Ta có .
nên hai vectơ cùng phương hay OA song song với BC và OA = BC = .
Do đó tứ giác OABC là hình bình hành.
Ta có hay OA OC
Tứ giác OABC là hình bình hành và có 1 góc vuông nên tứ giác OABC là hình chữ nhật.
b) Tâm I(x; y) của hình chữ nhật OABC là trung điểm của OB
Ta có
Vậy .
Xem thêm các bài giải sách bài tập Toán 10 bộ sách Chân trời sáng tạo hay, chi tiết khác:
Câu 1 trang 77 SBT Toán 10 Tập 2: Cho hai vectơ = (4; 3) và = (1; 7). Góc giữa hai vectơ và là...
Câu 3 trang 77 SBT Toán 10 Tập 2: Tam giác ABC có A = (– l; 1); B = (1; 3) và C = (1; –1). Trong các phát biểu sau đây, phát biểu nào đúng?...
Câu 4 trang 77 SBT Toán 10 Tập 2: Cho phương trình tham số của đường thẳng Trong các phương trình sau, phương trình nào là phương trình tổng quát của (d)?...
Câu 8 trang 78 SBT Toán 10 Tập 2: Phương trình tiếp tuyến tại điểm M(3; 4) với đường tròn (C): là...
Câu 11 trang 78 SBT Toán 10 Tập 2: Phương trình chính tắc của parabol có tiêu điểm (2; 0) là...
Bài 1 trang 78 SBT Toán 10 Tập 2: Trong mặt phẳng Oxy cho ba điểm A(2; 2); B(1; 3); C(– 1; 1). a) Chứng minh OABC là một hình chữ nhật...
Bài 2 trang 78 SBT Toán 10 Tập 2: Tìm góc giữa hai đường thẳng d1 và d2. a) và ...
Bài 5 trang 79 SBT Toán 10 Tập 2: Tính khoảng cách giữa hai đường thẳng:
Bài 6 trang 79 SBT Toán 10 Tập 2: Tìm tâm và bán kính của các đường tròn có phương trình: a) (x + 1)2 + (y + 2)2 = 225...
Bài 7 trang 79 SBT Toán 10 Tập 2: Lập phương trình đường tròn trong các trường hợp sau: a) Có tâm I(2; 2) và bán kính bằng 7...
Bài 8 trang 79 SBT Toán 10 Tập 2: Viết phương trình tiếp tuyến với đường tròn tại điểm A(4; 5)...
Bài 9 trang 79 SBT Toán 10 Tập 2: Gọi tên các đường conic sau...
Bài 11 trang 80 SBT Toán 10 Tập 2: Viết phương trình chính tắc của elip thoả mãn các điều kiện sau: a) Độ đài trục lớn 26; độ dài trục nhỏ 10...
Bài 13 trang 80 SBT Toán 10 Tập 2: Viết phương trình chính tắc của hypebol thoả mãn các điều kiện sau: a) Đỉnh (-6; 0) và (6; 0); tiêu điểm (-10; 0) và (10; 0)...
Bài 14 trang 80 SBT Toán 10 Tập 2: Tìm toạ độ tiêu điểm, phương trình đường chuẩn của các parabol sau: a) y2 = 4x...
Bài 15 trang 80 SBT Toán 10 Tập 2: Viết phương trình chính tắc của parabol thoả mãn các điều kiện: a) Tiêu điểm (8; 0)...
Bài 16 trang 80 SBT Toán 10 Tập 2: Một nhà mái vòm có mặt cắt hình nửa elip cao 6 m rộng l6 m. a) Hãy chọn hệ toạ độ thích hợp và viết phương trình của elip nói trên...
Bài viết liên quan
- Giải Sách bài tập Toán 10 Chân trời sáng tạo Bài 1: Tọa độ của vectơ
- Giải Sách bài tập Toán 10 Chân trời sáng tạo Bài 2: Đường thẳng trong mặt phẳng tọa độ
- Giải Sách bài tập Toán 10 Chân trời sáng tạo Bài 3: Đường tròn trong mặt phẳng tọa độ
- Giải Sách bài tập Toán 10 Chân trời sáng tạo Bài 4: Ba đường conic trong mặt phẳng tọa độ
- Giải Sách bài tập Toán 10 Chân trời sáng tạo Bài tập cuối chương 9
