Tìm các giá trị của tham số a, b, c để phương trình ax + by + c = 0 có thể biểu diễn được
Lời giải Bài 1 trang 65 SBT Toán 10 sách Chân trời sáng tạo hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 10.
Giải SBT Toán 10 Chân trời sáng tạo Bài 2: Đường thẳng trong mặt phẳng tọa độ
Bài 1 trang 65 SBT Toán 10 tập 2: Tìm các giá trị của tham số a, b, c để phương trình ax + by + c = 0 có thể biểu diễn được các đường thẳng trong hình đưới đây.
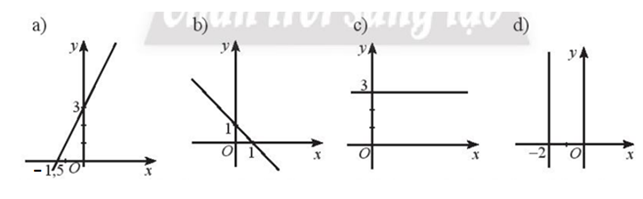
Lời giải:
a) Giả sử đường thẳng cần tìm có dạng y = a’x + b’
Đường thẳng đi qua điểm ; B(0; 3)
Ta có hệ
Suy ra đường thẳng có dạng y = 2x + 3 2x – y + 3 = 0
Vì vậy a = 2; b = – 1; c = 3.
b) Giả sử đường thẳng cần tìm có dạng y = a’x + b’
Đường thẳng đi qua điểm A(1; 0) ; B(0; 1)
Ta có hệ
Suy ra đường thẳng có dạng y = – x + 1 x + y – 1 = 0
Vì vậy a = 1; b = 1; c = – 1.
c) Giả sử đường thẳng cần tìm có dạng y = a’x + b’
Đường thẳng đi qua điểm A(0; 3) và song song với trục hoành nên đường thẳng có dạng y c 3 = 0
Vì vậy a = 0; b = 1; c = – 3.
d) Giả sử đường thẳng cần tìm có dạng y = a’x + b’
Đường thẳng đi qua điểm A(– 2; 0) và song song với trục Oy nên đường thẳng có dạng x + 2 = 0.
Vì vậy a = 1; b = 0; c = 2.
Xem thêm các bài giải sách bài tập Toán 10 bộ sách Chân trời sáng tạo hay, chi tiết khác:
Bài viết liên quan
- Giải Sách bài tập Toán 10 Chân trời sáng tạo Bài 1: Tọa độ của vectơ
- Giải Sách bài tập Toán 10 Chân trời sáng tạo Bài 2: Đường thẳng trong mặt phẳng tọa độ
- Giải Sách bài tập Toán 10 Chân trời sáng tạo Bài 3: Đường tròn trong mặt phẳng tọa độ
- Giải Sách bài tập Toán 10 Chân trời sáng tạo Bài 4: Ba đường conic trong mặt phẳng tọa độ
- Giải Sách bài tập Toán 10 Chân trời sáng tạo Bài tập cuối chương 9
