Ông An muốn thuê một chiếc ô tô (có lái xe) trong một tuần. Giá thuê xe được cho như bảng sau
Lời giải Bài 2.3 trang 25 Toán 10 sách Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 10.
Bài 2.3 trang 25 Toán 10 Tập 1: Ông An muốn thuê một chiếc ô tô (có lái xe) trong một tuần. Giá thuê xe được cho như bảng sau:
a) Gọi x và y lần lượt là số kilômét ông An đi trong các ngày từ thứ Hai đến thứ Sáu và trong hai ngày cuối tuần. Viết bất phương trình biểu thị mối liên hệ giữa x và y sao cho tổng số tiền ông An phải trả không quá 14 triệu đồng.
b) Biểu diễn miền nghiệm của bất phương trình ở câu a trên mặt phẳng tọa độ.
Lời giải
a) Số tiền ông An phải trả cho việc thuê xe ô tô từ thứ Hai đến thứ Sáu là:
900.5 + 8x = 4 500 + 8x (nghìn đồng).
Số tiền ông An phải trả cho việc thuê xe ô tô từ thứ Bảy và Chủ nhật là:
1 500.2 + 10y = 3 000 + 10y (nghìn đồng).
Tổng số tiền ông An phải trả cho việc thuê xe trong một tuần là:
4 500 + 8x + 3 000 + 10y = 7 500 + 8x + 10y (nghìn đồng).
Để tổng số tiền ông An phải trả không quá 14 triệu đồng thì
7 500 + 8x + 10y ≤ 14 000
⇔ 8x + 10y ≤ 6 500.
⇔ 4x + 5y ≤ 3 250.
Vậy bất phương trình biểu thị mối liên hệ giữa x và y sao cho tổng số tiền ông An phải trả không quá 14 triệu đồng là 4x + 5y ≤ 3 250.
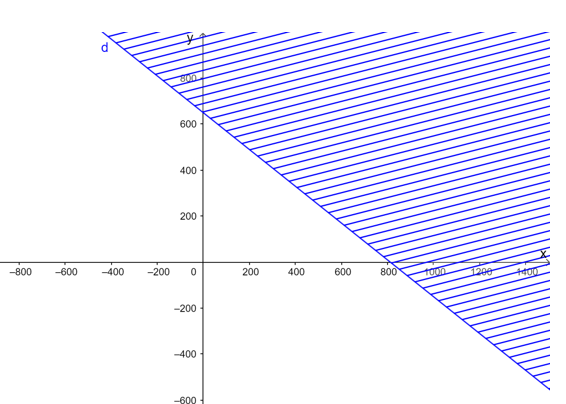
b)
Vẽ đường thẳng d: 4x + 5y = 3 250 trên mặt phẳng tọa độ.
Lấy gốc tọa độ O(0; 0) và tính 4.0 + 5.0 = 0 < 3 250.
Do đó miền nghiệm của bất phương trình là nửa mặt phẳng có bờ là đường thẳng d chứa gốc tọa độ và cả đường thẳng d (miền không bị gạch kể cả biên).
Bài viết liên quan
- Cho đường thẳng d: 2x – y = 4 trên mặt phẳng tọa độ Oxy (H.2.1). Đường thẳng này chia mặt phẳng thành hai nửa mặt phẳng
- Biểu diễn miền nghiệm của bất phương trình 2x + y < 200 trên mặt phẳng tọa độ
- Một công ty viễn thông tính phí 1 nghìn đồng mỗi phút gọi nội mạng và 2 nghìn đồng mỗi phút gọi ngoại mạng
- Bất phương trình nào sau đây là bất phương trình bậc nhất hai ẩn? a) 2x + 3y > 6
- Biểu diễn miền nghiệm của mỗi bất phương trình sau trên mặt phẳng tọa độ: a) 3x + 2y ≥ 300
