Giải bài tập Toán 10 Bài 13: Các số đặc trưng đo xu thế trung tâm

Mở đầu

Mở đầu trang 78 Toán 10 Tập 1: Hai phương pháp học Tiếng Anh khác nhau được áp dụng cho hai lớp A và B có trình độ tiếng Anh tương đương nhau. Sau hai tháng, điểm khảo sát tiếng Anh (thang điểm 10) của hai lớp được cho như hình bên.

Quan sát mẫu số liệu trên, có thể đánh giá được phương pháp học tập nào hiệu quả hơn không?

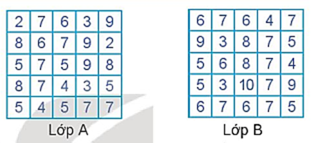
Lời giải:

Ta có thể đánh giá được phương pháp học tập nào hiệu quả hơn bằng cách tính toán các số đặc trưng (số trung bình cộng, số trung vị, tứ phân vị) cho mỗi mẫu số liệu rồi so sánh chúng với nhau.

Dưới đây phương pháp sử dụng số trung bình cộng:

Tổng điểm khảo sát Tiếng Anh của lớp A là:

2 + 7 + 6 + 3 + 9 + 8 + ... + 5 + 5 + 4 + 5 + 7 + 7 = 148 (điểm)

Tổng điểm khảo sát Tiếng Anh của lớp B là:

6 + 7 + 6 + 4 + 7 + 9 + ...+ 9 + 6 + 7 + 6 + 7 + 5 = 157 (điểm)

Trung bình cộng điểm khảo sát Tiếng Anh của lớp A là:

148 : 25 = 5,92 (điểm)

Trung bình cộng điểm khảo sát Tiếng Anh của lớp B là:

157 : 25 = 6,28 (điểm).

Vì 6,28 > 5,92 nên điểm trung bình của lớp B cao hơn điểm trung bình của lớp A.

Vậy phương pháp học tập được áp dụng ở lớp B hiệu quả hơn phương pháp được áp dụng ở lớp A.

1. Số trung bình và trung vị

HĐ 1 trang 78 Toán 10 Tập 1: Tính trung bình cộng điểm khảo sát Tiếng Anh của mỗi lớp A và B.

Lời giải:

Tổng điểm khảo sát Tiếng Anh của lớp A là:

2 + 7 + 6 + 3 + 9 + 8 + ... + 5 + 5 + 4 + 5 + 7 + 7 = 148 (điểm)

Tổng điểm khảo sát Tiếng Anh của lớp B là:

6 + 7 + 6 + 4 + 7 + 9 + ... + 9 + 6 + 7 + 6 + 7 + 5 = 157 (điểm)

Trung bình cộng điểm khảo sát Tiếng Anh của lớp A là:

148 : 25 = 5,92 (điểm)

Trung bình cộng điểm khảo sát Tiếng Anh của lớp B là:

157 : 25 = 6,28 (điểm)

Vậy trung bình cộng điểm tiếng Anh lớp A là 5,92 và lớp B là 6,28.

HĐ 2 trang 78 Toán 10 Tập 1: Dựa trên điểm trung bình, hãy cho biết phương pháp học tập nào hiệu quả hơn.

Lời giải:

Ta thấy điểm trung bình của lớp B cao hơn điểm trung bình của lớp A (vì 6,28 > 5,92).

Vậy phương pháp học tập được áp dụng ở lớp B hiệu quả hơn phương pháp được áp dụng ở lớp A.

Luyện tập 1 trang 78 Toán 10 Tập 1: Bảng sau cho biết thời gian chạy cự li 100 m của các bạn trong lớp (đơn vị giây):

Hãy tính thời gian chạy trung bình cự li 100 m của các bạn trong lớp.

Lời giải:

Số bạn trong lớp là:

5 + 7 + 10 + 8 + 6 = 36 (bạn).
Thời gian chạy trung bình cự li 100 m của các bạn trong lớp là:

$\overline{X}=\frac{12.5+13.7+14.10+15.8+16.6}{36}\approx 14,08$ (giây).

Vậy thời gian chạy trung bình cự li 100 m của các bạn trong lớp là khoảng 14,08 giây.

HĐ 3 trang 79 Toán 10 Tập 1: Một công ty nhỏ gồm 1 giám đốc và 5 nhân viên, thu nhập mỗi tháng của giám đốc là 20 triệu đồng, của nhân viên là 4 triệu đồng.

a) Tính thu nhập trung bình của các thành viên trong công ty.

b) Thu nhập trung bình có phản ánh đúng thu nhập của nhân viên trong công ty không?

Lời giải

a) Thu nhập trung bình của thành viên trong công ty là:

$\overline{X}=\frac{20.1+4.5}{6}=\frac{40}{6}\approx 6,67$ (triệu đồng).

Vậy thu nhập trung bình của các thành viên trong công ty khoảng 6,67 triệu đồng.

b) Ta thấy rõ ràng thu nhập của giám đốc cao hơn thu nhập trung bình rất nhiều (khoảng 13,3 triệu), còn thu nhập của mỗi nhân viên thì gần với thu nhập trung bình hơn (khoảng 2,67 triệu).

Do đó, thu nhập trung bình không phản ánh đúng thu nhập của nhân viên công ty.

Luyện tập 2 trang 79 Toán 10 Tập 1: Chiều dài (đơn vị feet) của 7 con cá voi trưởng thành được cho như sau:

48      53      51      31      53      112    52.

Tìm số trung bình và số trung vị của mẫu số liệu trên. Trong hai số đó, số nào phù hợp hơn để đại diện cho chiều dài của 7 con cá voi trưởng thành này?

Lời giải:

Số trung bình của mẫu số liệu trên là:

$\overline{X}=\frac{48+53+51+31+53+112+52}{7}=\frac{400}{7}\approx 57,14.$

Sắp xếp số liệu trên theo thứ tự không giảm, ta được:

31; 48; 51; 52; 53; 53; 112.

Số giá trị là 7 và là số lẻ nên giá trị chính giữa của mẫu là trung vị.

Do đó, số trung vị của mẫu số liệu trên là 52.

Ta thấy trong mẫu số liệu bài cho thì 112 cao hơn hẳn giá trị trung bình nên không thể dùng số trung bình để đại diện cho chiều dài của 7 con cá voi trưởng thành này.

Vậy trong hai số trên, số đại diện cho chiều dài của 7 con cá voi trưởng thành là số trung vị 52.

2. Tứ phân vị

HĐ 4 trang 80 Toán 10 Tập 1: Điểm (thang điểm 100) của 12 thí sinh cao điểm nhất trong cuộc thi như sau:

58      74      92      81      97      88      75      69      87      69      75      77.

Ban tổ chức muốn trao các giải Nhất, Nhì, Ba, Tư cho các thí sinh này, mỗi giải trao 25% số thí sinh (3 thí sinh).

Em hãy giúp ban tổ chức xác định các ngưỡng điểm để phân loại thí sinh.

Lời giải:

Sắp xếp dãy số liệu trên theo thứ tự không giảm, ta được:

58; 69; 69; 74; 75; 75; 77; 81; 87; 88; 92; 97.

Mỗi giải có 3 thí sinh nên ta sẽ xếp lần lượt các thí sinh vào các nhóm giải dựa vào số điểm thi của thí sinh như sau:

Nhóm giải tư: 58; 69; 69.

Nhóm giải ba: 74; 75; 75.

Nhóm giải nhì: 77; 81; 87.

Nhóm giải nhất: 88; 92; 97.

Giữa các nhóm giải ta xác định được các ngưỡng điểm để phân loại thí sinh:

∙ Ngưỡng điểm phân loại giữa nhóm giải tư và nhóm giải ba là:

(69 + 74) : 2 = 71,5.

∙ Ngưỡng điểm phân loại giữa nhóm giải ba và nhóm giải nhì là:

(75 + 77) : 2 = 76.

∙ Ngưỡng điểm phân loại giữa nhóm giải nhì và nhóm giải nhất là:

(87 + 88) : 2 = 87,5.

Vậy ba ngưỡng điểm giúp ban tổ chức phân loại thí sinh là: 71,5; 76; 87,5.

Luyện tập 3 trang 81 Toán 10 Tập 1: Bảng sau đây cho biết số lần học tiếng Anh trên Internet trong một tuần của một số học sinh lớp 10:

Hãy tìm các tứ phân vị cho mẫu số liệu này.

Lời giải:

Ta có: n = 2 + 4 + 6 + 12 + 8 + 3 = 35.

Vì n = 35 là số lẻ nên trung vị Q₂ là số ở vị trí số 18

Ta thấy 2 + 4 + 6 < 18 < 2 + 4 + 6 + 12.

Do đó Q₂ = 3.

Ta tìm Q₁ là trung vị của nửa số liệu bên trái Q₂ (không bao gồm Q₂).

Nửa số liệu bên trái Q₂ có 17 học sinh nên trung vị là học sinh thứ 9.

Ta thấy 2 + 4 < 9 < 2 + 4 + 6.

Do đó Q₁ = 2.

Ta tìm Q₃ là trung vị của nửa số liệu bên phải Q₂ (không bao gồm Q₂)

Nửa số liệu bên phải Q₂ có 17 học sinh nên trung vị là học sinh thứ 9 trong 17 học sinh và là học sinh thứ 9 + 18 = 27 trong 35 học sinh.

Ta thấy 2 + 4 + 6 + 12 < 27 < 2 + 4 + 6 + 12 + 8.

Do đó Q₃ = 4.

Vậy tứ phân vị cho mẫu số liệu này là Q₁ = 2; Q₂ = 3, Q₃ = 4.

3. Mốt

HĐ 5 trang 81 Toán 10 Tập 1: Một cửa hàng giày thể thao đã thống kê cỡ giày của một số khách hàng nam được chọn ngẫu nhiên cho kết quả như sau:

38   39   39   38   40   41   39   39   38   39   39   39   40   39   39.

a) Tính cỡ giày trung bình. Số trung bình này có ý nghĩa gì với cửa hàng không?

b) Cửa hàng nên nhập cỡ giày nào với số lượng nhiều nhất?

Lời giải:

a) Bảng tần số:

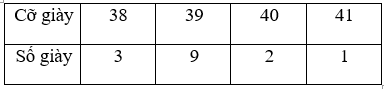
Cỡ giày trung bình:

$\overline{X}=\frac{38.3+39.9+40.2+41}{3+9+2+1}=\frac{586}{15}\approx 39,07$

Ý nghĩa: Cỡ giày trung bình này có thể đại diện cho cỡ giày của cửa hàng hay nói cách khác là cửa hàng bán được nhiều cỡ giày 39 nhất.

b) Cỡ giày số 39 là cỡ giày nhiều khách nam đi nhất trong tổng số người được chọn nên cửa hàng nên nhập cỡ giày này.

Vận dụng trang 82 Toán 10 Tập 1: Hãy tính các số đặc trưng đo xu thế trung tâm cho mẫu số liệu về điểm khảo sát của lớp A và lớp B ở đầu bài để phân tích và so sánh hiệu quả học tập của hai phương pháp này.

Lời giải:

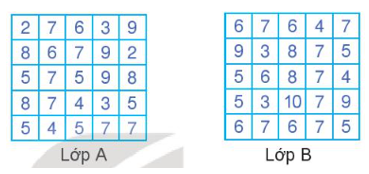
* Xét lớp A:

Bảng tần số: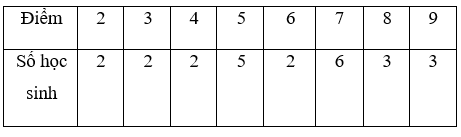

Trung bình cộng điểm khảo sát Tiếng Anh của lớp A là:

$$\begin{gathered} \frac{2.2+3.2+4.2+5.5+6.2+7.6+8.3+9.3}{2.4+5+6+3.2} \\ =\frac{148}{25}=5,92 \end{gathered}$$

Vì n = 25 nên trung vị: số thứ 13.
Ta thấy: 2 + 2 + 2 + 5 + 2 = 13.

Do đó trung vị là 6.

Từ bảng tần số, ta thấy điểm 7 xuất hiện nhiều nhất (6 lần).

Do đó mốt của số liệu là 7.

* Xét lớp B:

Bảng tần số:

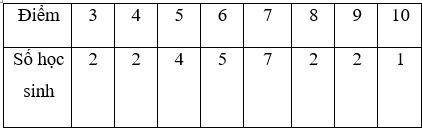 Trung bình cộng điểm khảo sát Tiếng Anh của lớp B là:

$$\begin{gathered} \frac{3.2+4.2+5.4+6.5+7.7+8.2+9.2+10.1}{2.4+4+5+7+1} \\ =\frac{157}{25}=6,28 \end{gathered}$$

Vì n = 25 nên trung vị: số thứ 13.

Ta thấy 2 + 2 + 4 + 5 = 13.

Do đó trung vị là 6.

Từ bảng tần số, ta thấy điểm 7 xuất hiện nhiều nhất (7 lần).

Do đó mốt của số liệu là 7.

Ta thấy:

+ Điểm trung bình của lớp B cao hơn điểm trung bình của lớp A (vì 6,28 > 5,92).

Do đó phương pháp học tập được áp dụng ở lớp B hiệu quả hơn phương pháp được áp dụng ở lớp A.

+ Số trung vị của hai dãy số liệu là bằng nhau nên nếu dùng số trung vị thì không thể so sánh được hiệu quả học tập của hai phương pháp này.

+ Mốt của hai dãy số liệu là bằng nhau nên nếu dùng mốt thì không thể so sánh được hiệu quả học tập của hai phương pháp này.

Bài tập

Bài 5.7 trang 82 Toán 10 Tập 1: Tìm số trung bình, trung vị, mốt và tứ phân vị của mỗi mẫu số liệu sau đây:

a) Số điểm mà năm vận động viên bóng rổ ghi được trong một trận đấu:

9        8        15      8        20

b) Giá của một số loại giày (đơn vị nghìn đồng):

350    300    650    300    450    500    300    250

c) Số kênh được chiếu của một số hãng truyền hình cáp:

36      38      33      34      32      30      34      35

Lời giải:

a) Số điểm mà năm vận động viên bóng rổ ghi được trong một trận đấu:

9        8        15      8        20

Số trung bình:

$\overline{X}=\frac{9+8+15+8+20}{5}=12$

Trung vị:

Mẫu số liệu sắp xếp theo thứ tự không giảm, ta được:

8; 8; 9; 15; 20

Ta có n = 5 là số lẻ nên trung vị là 9.

∙ Mốt:

Ta thấy số 8 là số có tần số lớn nhất (xuất hiện 2 lần).

Do đó mốt của số liệu là 8.

∙ Tứ phân vị:

+ Tìm Q₂.

Ta có trung vị là 9 nên Q₂ = 9.

+ Tìm Q₁.

Nửa số liệu bên trái là: 8 8

Trung vị của mẫu này là: (8 + 8) : 2 = 8

Do đó Q₁ = 8.

 + Tìm Q₃.

Nửa số liệu bên phải là: 15  20

Trung vị của mẫu này là: (15 + 20) : 2 = 17,5.

Do đó Q₃ = 17,5.

Vậy số trung bình là 12; trung vị là 9; mốt là 8; Q₁ = 8; Q₃ = 17,5.

b) Giá của một số loại giày (đơn vị nghìn đồng):

350    300    650    300    450    500    300    250

∙ Số trung bình:

$$\begin{gathered} \overline{X}=\frac{350+300+650+300+450+500+300+250}{8} \\ =387,5 \end{gathered}$$

∙ Trung vị:

Mẫu số liệu sắp xếp theo thứ tự không giảm ta được:

250; 300; 300; 300; 350; 450; 500; 650.

Ta có n = 8 là số chẵn nên trung vị là trung bình cộng của hai số chính giữa.

Số trung bình cộng của hai giá trị ở chính giữa là:

(300 + 350) : 2 = 325.

Do đó trung vị là 325.

∙ Mốt:

Ta thấy số 300 là số có tần số cao nhất (xuất hiện 3 lần).
Do đó mốt của dãy số liệu là 300.

∙ Tứ phân vị:

+ Tìm Q₂.

Ta có trung vị là 325.

Do đó Q₂ = 325.

+ Tìm Q₁.

Vì n chẵn nên nửa số liệu bên trái là: 250  300  300  300

Trung vị của mẫu này là: (300 + 300) : 2 = 300

Do đó Q₁ = 300.

+ Tìm Q₃.

Vì n chẵn nên nửa số liệu bên phải là: 350  450  500  650

Trung vị của mẫu này là: (450 + 500) : 2 = 475

Do đó Q₃ = 475.

Vậy số trung bình là 387,5; trung vị là 325; mốt là 300; Q₁ = 300; Q₃ = 475.

c) Số kênh được chiếu của một số hãng truyền hình cáp:

36  38  33  34  32  30  34  35

∙ Số trung bình:

$\overline{X}=\frac{36+38+33+34+32+30+34+35}{8}=34$

∙ Trung vị:

Sắp xếp theo thứ tự không giảm: 30  32  33  34  34  35  36  38

Ta có n = 8 là số chẵn nên trung vị là trung bình cộng của hai số chính giữa.

Hai số chính giữa là 34 và 34.

Do đó trung vị là: (34 + 34) : 2 = 34.

∙ Mốt:

Ta thấy số 34 là số có tần số cao nhất (xuất hiện 2 lần).

Do đó mốt của dãy số liệu là 34.

∙ Tứ phân vị:

+ Tìm Q₂.

Ta có trung vị là 34.

Do đó Q₂ = 34.

+ Tìm Q₁.

Vì n chẵn nên nửa số liệu bên trái là: 30  32  33  34

Trung vị của mẫu này là: (32 + 33) : 2 = 32,5

Do đó Q₁ = 32,5.

+ Tìm Q₃.

Vì n chẵn nên nửa số liệu bên phải là: 34  35  36  38

Trung vị của mẫu này là: (35 + 36) : 2 = 35,5

Do đó Q₃ = 35,5.

Vậy số trung bình là 34; trung vị là 34; mốt là 34; Q₁ = 32,5; Q₃ = 35,5.

Bài 5.8 trang 82 Toán 10 Tập 1: Hãy chọn số đặc trưng đo xu thế trung tâm của mỗi mẫu số liệu sau. Giải thích và tính các giá trị của số đặc trưng đó.

a) Số mặt trăng đã biết của các hành tinh:

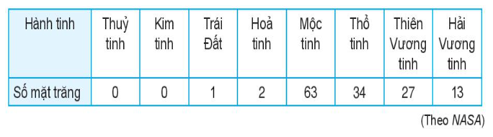
b) Số đường chuyền thành công trong một trận đấu của một số cầu thủ bóng đá:

32   24   20   14   23.

c) Chỉ số IQ của một nhóm học sinh:

80   102   83   103   108   94   110   106   104   100.

d) Các sai số trong một phép đo:

10   15   18   15   14   13   42   15   12   14   42.

Lời giải:

a) Sắp xếp lại số liệu:

0   0   1   2   13   27   34   63

Trung vị là: (2 + 13) : 2 = 7,5.

Ta không chọn số trung bình vì số trung bình là 17,5 chênh lệch với 63 lớn. Mốt cũng thế.

b) Các số liệu bài cho không chênh lệch quá lớn với số trung bình nên ta chọn số trung bình.

Số đường truyền trung bình là:

$\frac{32+24+20+14+23}{5}=22,6$

c) Các số liệu bài cho không chênh lệch quá lớn với số trung bình nên ta chọn số trung bình.

Chỉ số IQ trung bình của nhóm học sinh là: 

$\frac{60+72+63+83+68+74+90+86+74+80}{10}=75.$

d) Ta thấy 42 chênh lệch lớn với các số còn lại nên ta chọn Mốt để đo xu thế trung tâm.

Mốt là 15 (tần số là 3).

Bài 5.9 trang 83 Toán 10 Tập 1: Số học sinh giỏi Quốc gia năm 2018 – 2019 của 10 trường Trung học phổ thông được cho như sau:

0  0  4  0  0  0  10  0  6  0.

a) Tìm số trung bình, mốt, các tứ phân vị của mẫu số liệu trên.

b) Giải thích tại sao tứ phân vị thứ nhất và trung vị trùng nhau.

Lời giải:

a)

∙ Số trung bình:

Trung bình số lượng học sinh giỏi Quốc gia của 10 trường Trung học phổ thông là:

$\frac{0.7+4+6+10}{10}=2$

∙ Mốt:

Trong dãy số liệu đã cho, số 0 là số xuất hiện với tần số lớn nhất (7 lần).

Do đó mốt của số liệu là 0.

∙ Trung vị:

Sắp xếp dãy số liệu trên theo thứ tự không giảm là:

0; 0; 0; 0; 0; 0; 0; 4; 6; 10.

Vì n = 10 là số chẵn nên Q₂ là trung bình cộng của hai giá trị chính giữa:

 Q₂ = (0 + 0) : 2 = 0.

∙ Tứ phân vị:

Ta tìm Q₁ là trung vị của nửa số liệu bên trái Q₂:

0; 0; 0; 0 ;0.

Do đó Q₁ = 0.

Ta tìm Q₃ là trung vị của nửa số liệu bên phải Q₂:

0; 0; 4; 6; 10.

Do đó Q₃ = 4.

Vậy số trung bình là 2; mốt là 0, tứ phân vị là Q₁ = 0; Q₂ = 0; Q₃ = 4.

b) Tứ phân vị thứ nhất và trung vị trùng nhau vì mật độ của mẫu số liệu tập trung hết ở nửa trái của trung vị, mẫu số liệu bên trái có số liệu bằng 0 hết.

Bài 5.10 trang 83 Toán 10 Tập 1: Bảng sau đây cho biết số chỗ ngồi của một số sân vận động được sử dụng trong Giải Bóng đá Vô địch Quốc gia Việt Nam năm 2018 (số liệu gần đúng).

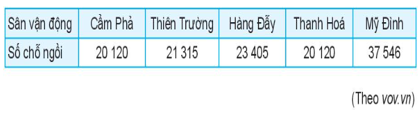
Các giá trị số trung bình, trung vị, mốt bị ảnh hưởng thế nào nếu bỏ đi số liệu chỗ ngồi của Sân vận động Quốc gia Mỹ Đình?

Lời giải:

Dãy số liệu sắp xếp theo thứ tự không giảm là:

20 120; 20 120; 21 315; 23 405; 37 546.

Số trung bình

$\frac{20120.2+21315+23405+37546}{5}=24501,2$

Số chỗ ngồi trung bình của một sân vận động được sử dụng trong Giải Bóng đá Vô địch Quốc gia Việt Nam là:

$\frac{20120.2+21315+23405+20120+37546}{5}=24501,2.$

Vì n = 5 là số lẻ nên số trung vị của dãy số liệu là số chính giữa là: 21 315.

Số 20 120 là số xuất hiện nhiều nhất nên mốt của số liệu là 20 120.

Nếu bớt đi số liệu chỗ ngồi của Sân vận động Quốc gia Mỹ Đình, ta có:

Số chỗ ngồi trung bình của một sân vận động được sử dụng trong Giải Bóng đá Vô địch Quốc gia Việt Nam là:

$\frac{20120+21315+23405+20120}{4}=21240.$

Dãy số liệu sắp xếp theo thứ tự không giảm là:

20 120; 20 120; 21 315; 23 405.

Vì n = 4 là số chẵn nên số trung vị của dãy số liệu là trung bình cộng hai giá trị chính giữa là: (20 120 + 21 315) : 2 = 20 717,5.

Số 20 120 là số xuất hiện nhiều nhất nên mốt của số liệu là 20 120.

Vậy khi bỏ bớt đi số liệu chỗ ngồi của Sân vận động Quốc gia Mỹ Đình thì số trung bình và trung vị bị thay đổi còn mốt vẫn giữ nguyên