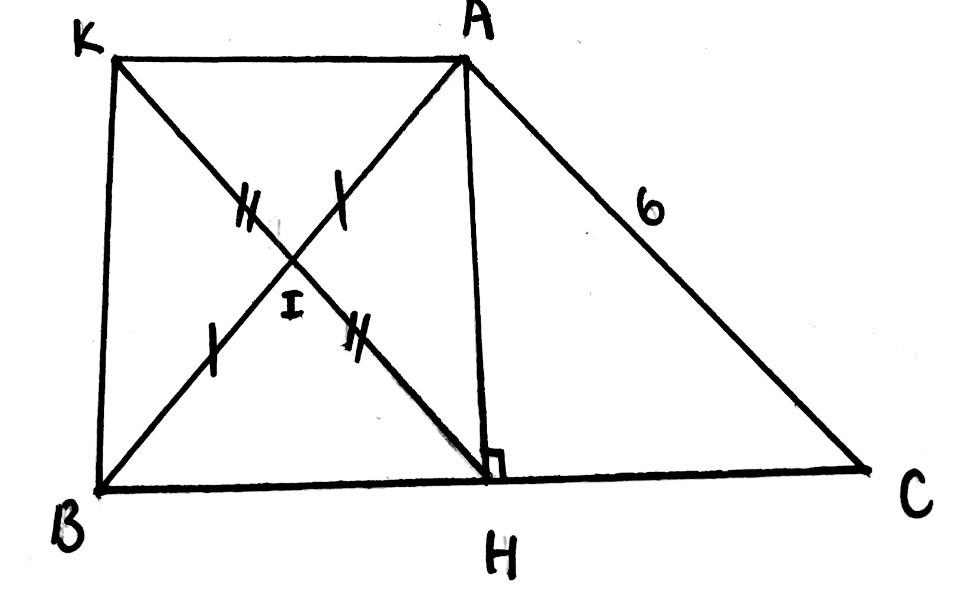
Cho tam giác ABC cân tại A, đường cao AH. Gọi I là trung điểm của AB, K là
điểm đối xứng của H qua I.
a) Cho biết AC = 6 cm. Tính IH.
b) Chứng minh tứ giác AHBK là hình chữ nhật.
c) Tam giác ABC có thêm điều kiện gì thì hình chữ nhật AHBK là hình vuông?
Quảng cáo
2 câu trả lời 3420
 @hoccungbemikey
@hoccungbemikey
a)
*Xét ABC cân ở A (gt)
AB = AC
→ AB = AC = 6 cm
*Có AH là đg cao (gt)
→ AH BC
→ AHB vuông ở H
→ IH = (đlý đg trung tuyến ứng với cạnh huyền)
→ IH = (cm)
b)
* Có K đối xứng H qua I (gt)
→ I là tđ KH (tc)
*Xét tứ giác AHBK có:
→ AHBK là hbh (DHNB) (1)
có AH ⊥ BC (cmt) (2)
* Từ (1) và (2) → AHBK là hcn (DHNB)
c)
AHBK là hcn (cm câu b)
→ AHBK là hình vuông hcn AHBK + BH = AH (theo DHNB)
+ Trong △ ABC cân ở A có đg cao AH (gt)
→ AH cũng là trung tuyến (tc)
→ H là tđ BC
→ BH = HC = BC
+ Có BH = AH (điều kiện cho thêm)
→ BH = AH = BC
→ AH = BC
→ AH là trung tuyến ứng với một cạnh
→ △ABC vuông ở A (định lí trung tuyến ứng với cạnh huyền)
mà có △ABC cân ở A (gt)
→ △ABC vuông cân ở A
1Kết luận: AHBK là hình vuông 2△ABC vuông cân ở A
chúc em học tốt
Quảng cáo
Bạn cần hỏi gì?
Câu hỏi hot cùng chủ đề
-
107593
-
Hỏi từ APP VIETJACK
 Đã trả lời bởi chuyên gia
68300
Đã trả lời bởi chuyên gia
68300 -
 Đã trả lời bởi chuyên gia
52884
Đã trả lời bởi chuyên gia
52884 -
 Đã trả lời bởi chuyên gia
47390
Đã trả lời bởi chuyên gia
47390 -
 Đã trả lời bởi chuyên gia
45461
Đã trả lời bởi chuyên gia
45461 -
 Đã trả lời bởi chuyên gia
45109
Đã trả lời bởi chuyên gia
45109 -
Hỏi từ APP VIETJACK
 Đã trả lời bởi chuyên gia
38488
Đã trả lời bởi chuyên gia
38488 -
 Đã trả lời bởi chuyên gia
38230
Đã trả lời bởi chuyên gia
38230


