Bài 3. Cho tam giác ABC, các đường trung tuyến AD, BE, CF, trong đó AD vuông góc với BE, AD = 3cm, BE = 4cm.
a) Lấy điểm K sao cho D là trung điểm của EK. Chứng minh AFKD là hình bình hành
b) Tinh độ dài đoạn CF.
Bài 4. Cho tam giác ABC, trực tâm H. Gọi M là trung điểm của BC. Các đường trung trực của AC và BC cắt nhau tại O. Trên tia đối của tia OC lấy điểm K sao cho OK = OC. CMR:
a) Tứ giác AHBK là hình bình hành
b) OM= 1/2 AH
mn giúp e ạ, e cần gấp, hứa 5* ạ
Quảng cáo
1 câu trả lời 2048
Theo quy định mỗi lần chỉ hỏi 1 bài thôi em nhé
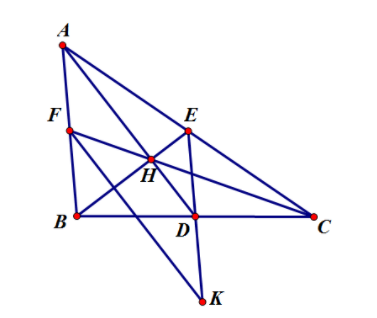
Bài 3:
a)Xét tam giác BAC có E;D là trung điểm AC và BC
=> ED là đường trung bình tam giác BAC
=> ED//AB và ED=BA2
Mà F là trung điểm AB; D là trung điểm EK
=> AF//DK;AF=DK
Xét tứ giác AFDK có:AF//DK;AF=DK
=> Tú giác AFDK là hbh
b) Gọi H là giao điểm của AD;BE;CF
=> H là trọng tâm tam giác ABC
AH=23AD=23.4=83(cm)BH=23BE=23.3=2(cm)
xét tam giác ABH vuông tại H
Theo Pytago:
AB2=AH2+BH2=(83)2+22=>AB=103(cm)
Có HF là đường trjng tuyến ứng với cạnh huyền AB
=> HF=AB2=53(cm)
Do H là trọng tâm tam giác ABC
=> CF=3HF=5 cm
vậy CF=5cm
Quảng cáo
Câu hỏi hot cùng chủ đề
-
5 85939
-
Hỏi từ APP VIETJACK7 44628
-
Cho tam giác MNP vuông tại M,đường cao MH
a, Chứng minh tam giác HMN đồng dạng với tam giác MNP
b, chứng minh hệ thức MH2=NH.PH
c, Lấy điểm E tùy ý trên cạnh MP,vẽ điểm F trên cạnh MN sao cho góc FHE =90 độ. Chứng minh tam giác NFH đồng dạng với tam giác MEH và góc NMH=góc FEH
d,Xác định vị trí điểm E trên MP sao cho diện tích tam giác HEF đạt giá trị nhỏ nhất
6 38303


