Cho hình thang cân ABCD, đáy nhỏ AB, đáy lớn CD.Góc nhọn hợp bởi hai đường chéo AC và BD bằng 60 độ. Gọi M,N là hình chiếu của B và C lên AC và BD. P là trung điểm BC.Chứng minh tam giác MNP đều Mọi người làm giúp e , tối nay e phải nộp rồi ạ, hứa 5* ạ
Quảng cáo
2 câu trả lời 2533
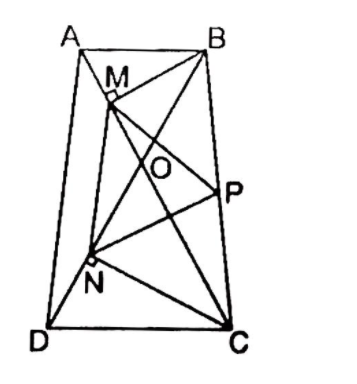
Vì ABCD là hình thang cân nên tam giác AOB cân tại O
mà : góc AOB = 60 độ
=> tam giác AOB đều, tam giác COD đều
Mặt khác:
BM là đường cao của tam giác AOB
=> BM cũng là trung tuyến
=> MA = MO
CN là đường cao của tam giác COD
=> CN cũng là trung tuyến
=> NO = ND
Tam giác AOD có :
MA = MO, NO = ND
=> MN = AD:2
Tam giác BMC vuông tại M có MP là trung tuyến nên MP = BC:2 = AD:2
Tam giác BNC vuông tại N có NP là trung tuyến nên NP = BC:2 = AD:2
Do đó : MN = NP = MP
=> MNP là tam giác đều
Vậy MNP là tam giác đều
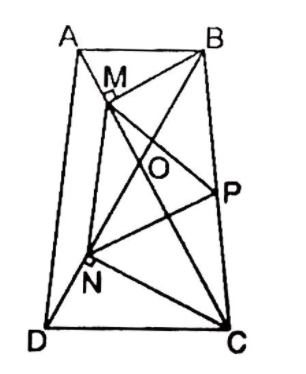
Xét hình thang cân ABCD có Ac cắt BD tại O
=> OA=OB; OC=OD; AD=BC ( tính chất hình thang cân)
Xét tam giác OAB có OA=OB; góc AOB=60
=> Tam giác OAB đều
Có BM là đường cao
=> BM đồng thời là trung tuyến
=> M là trung điểm của AO
Chứng minh tương tự có N laf trung điểm của OD
Xét tam giác AOD có M; N là trung điểm AO;OD
=> MN là đường trung bình của tam giác AOD
=> MN=AD/2( tính chất đường trung bình tam giác )
Mà AD=BC
P là trung điểm BC (gt)
=> MN=BC/2
Xét tam giác BMC vuông tại M
có MP là trung tuyến
=> MP=BC/2(tính chất trung tuyến ứng với cạnh huyền tam giác vuông bằng nửa canht huyền)
Xét tam giác BNC vuông tại N có NP là trung tuyến
=> PN=BC/2(tính chất trung tuyến ứng với cạnh huyền tam giác vuông bằng nửa canht huyền)
Xét tam giác MNP có: MN=NP=MP
=> Tam giác MNP đều
Vậy tam giác MNP đều
Quảng cáo
Câu hỏi hot cùng chủ đề
-
5 85939
-
Hỏi từ APP VIETJACK7 44628
-
Cho tam giác MNP vuông tại M,đường cao MH
a, Chứng minh tam giác HMN đồng dạng với tam giác MNP
b, chứng minh hệ thức MH2=NH.PH
c, Lấy điểm E tùy ý trên cạnh MP,vẽ điểm F trên cạnh MN sao cho góc FHE =90 độ. Chứng minh tam giác NFH đồng dạng với tam giác MEH và góc NMH=góc FEH
d,Xác định vị trí điểm E trên MP sao cho diện tích tam giác HEF đạt giá trị nhỏ nhất
6 38303


