Đề bài:
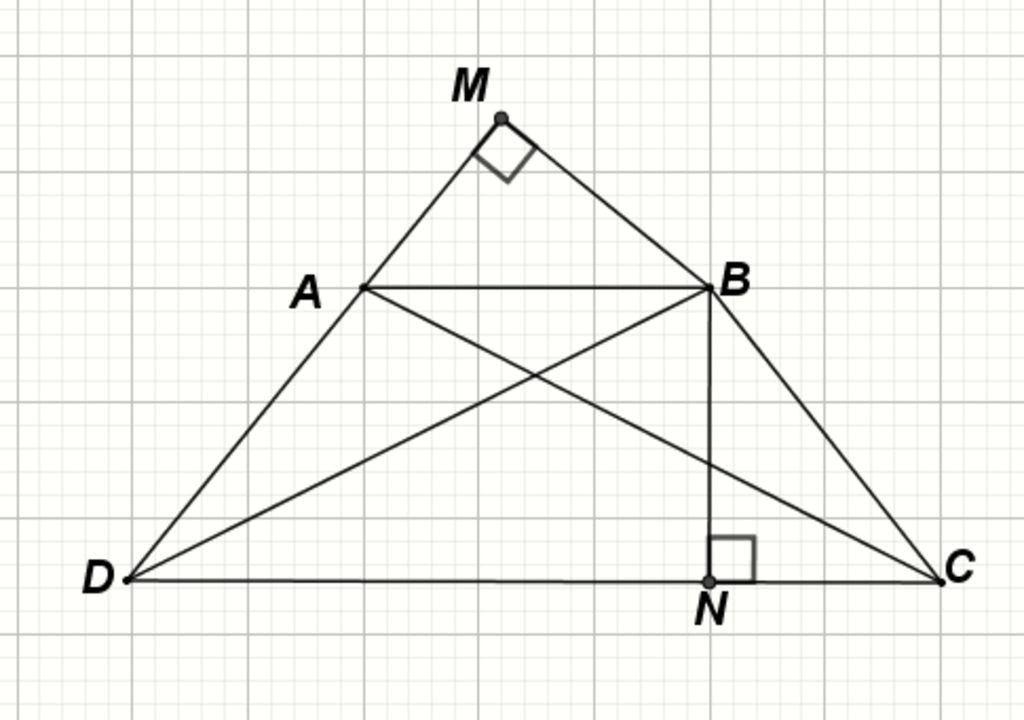
Cho tứ giác ABCD có:

AD=AB=BCAD = AB = BCAD=AB=BC
∠A+∠C=180∘\angle A + \angle C = 180^\circ∠A+∠C=180∘
Chứng minh:

a) DBDBDB là tia phân giác của góc ∠D\angle D∠D

b) Tứ giác ABCDABCDABCD là hình thang cân

Phân tích ban đầu:
Cho:

AD=AB=BCAD = AB = BCAD=AB=BC → 3 cạnh bằng nhau:
Tức là △ABD\triangle ABD△ABD và △DBC\triangle DBC△DBC có các cạnh bằng nhau.
∠A+∠C=180∘\angle A + \angle C = 180^\circ∠A+∠C=180∘ → Dấu hiệu tứ giác nội tiếp

a) Chứng minh: DBDBDB là tia phân giác của ∠D\angle D∠D
Xét tam giác △ABD\triangle ABD△ABD và △CBD\triangle CBD△CBD:
Ta có:

AB=ADAB = ADAB=AD (giả thiết)
BC=AB⇒AB=BC⇒AD=BCBC = AB \Rightarrow AB = BC \Rightarrow AD = BCBC=AB⇒AB=BC⇒AD=BC
→ Suy ra AD=AB=BCAD = AB = BCAD=AB=BC
Xét hai tam giác △ABD\triangle ABD△ABD và △CBD\triangle CBD△CBD:
AB=BCAB = BCAB=BC (giả thiết)
AD=DCAD = DCAD=DC (vì AD=BCAD = BCAD=BC, AB=BCAB = BCAB=BC, nên AD=DCAD = DCAD=DC)
Chung cạnh BDBDBD
→ Hai tam giác ABDABDABD và CBDCBDCBD cân tại A và C, lại có các cạnh liên quan bằng nhau.

Ý tưởng chính:
Từ các điều kiện, ta nhận thấy tam giác △ABD\triangle ABD△ABD và △DBC\triangle DBC△DBC cân tại A và C, nên:

∠ABD=∠DAB\angle ABD = \angle DAB∠ABD=∠DAB
∠CBD=∠DCB\angle CBD = \angle DCB∠CBD=∠DCB
Mà đề cho ∠A+∠C=180∘\angle A + \angle C = 180^\circ∠A+∠C=180∘

→ Khi đó:

∠DAB+∠DCB=180∘⇒∠ABD+∠CBD=180∘\angle DAB + \angle DCB = 180^\circ \Rightarrow \angle ABD + \angle CBD = 180^\circ∠DAB+∠DCB=180∘⇒∠ABD+∠CBD=180∘→ Tam giác △DBC\triangle DBC△DBC và △ABD\triangle ABD△ABD có các góc tại B bù nhau

→ Vậy góc ∠ABD=∠CBD\angle ABD = \angle CBD∠ABD=∠CBD

→ Suy ra DBDBDB là tia phân giác của ∠D\angle D∠D

✅ Kết luận a:
DB laˋ tia phaˆn giaˊc của ∠D\boxed{DB \text{ là tia phân giác của } \angle D}DB laˋ tia phaˆn giaˊc của ∠D​
b) Chứng minh tứ giác ABCDABCDABCD là hình thang cân

Từ giả thiết:
∠A+∠C=180∘\angle A + \angle C = 180^\circ∠A+∠C=180∘ → ABCDABCDABCD là tứ giác nội tiếp
AB=DCAB = DCAB=DC, AD=BCAD = BCAD=BC (vì cả 3 cạnh bằng nhau)

Xét 2 cạnh đối AD và BC:
AD=BCAD = BCAD=BC (giả thiết)
AB=DCAB = DCAB=DC (vì đều bằng AD)
→ Tứ giác có 2 cạnh bên bằng nhau và ∠A+∠C=180∘\angle A + \angle C = 180^\circ∠A+∠C=180∘

→ Suy ra: ABCD là hình thang, vì 2 góc kề một đáy bù nhau

Mà 2 cạnh bên AD = BC, nên hình thang cân

✅ Kết luận b:
ABCD laˋ hıˋnh thang caˆn\boxed{ABCD \text{ là hình thang cân}}ABCD laˋ hıˋnh thang caˆn​
✅ Tổng kết đáp án:
a) DB laˋ tia phaˆn giaˊc của ∠D\boxed{DB \text{ là tia phân giác của } \angle D}DB laˋ tia phaˆn giaˊc của ∠D​
b) ABCD laˋ hıˋnh thang caˆn\boxed{ABCD \text{ là hình thang cân}}ABCD laˋ hıˋnh thang caˆn​